
23.(坐标系与参数方程选做题)(本题满分10分)
已知圆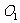 和圆
和圆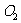 的极坐标方程分别是
的极坐标方程分别是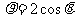 和
和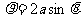 (
(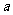 是非零常数)
是非零常数)
(1)将两圆的极坐标方程化为直角坐标方程;
(2)若两圆的圆心距为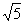 ,求
,求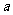 的值.
的值.
|
22.(几何证明选讲选做题)(本题满分10分)
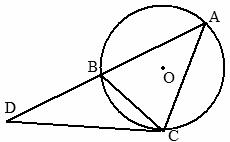
如图,圆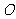 是
是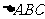 的外接圆.过点
的外接圆.过点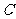 的切线交
的切线交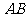 的延长线于点
的延长线于点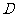 ,
,
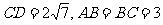 ,求
,求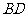 以及
以及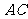 的长.
的长.
21.(本题满分14分)
已知函数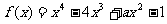 在区间
在区间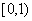 上单调递增,在区间
上单调递增,在区间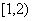 上单调递减.
上单调递减.
(1)求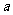 的值;
的值;
(2)若点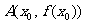 在函数
在函数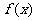 的图象上,求证:点
的图象上,求证:点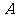 关于直线
关于直线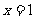 的对称点
的对称点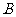 也在函数
也在函数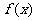 的图象上;
的图象上;
(3)问是否存在实数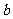 ,使函数
,使函数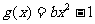 的图象与函数
的图象与函数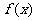 的图象恰好有3个交点?若存在,请求出
的图象恰好有3个交点?若存在,请求出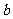 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
20.(本题满分12分)
已知等差数列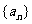 前三项分别是
前三项分别是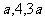 ,前
,前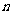 项和为
项和为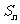 ,且
,且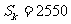 ,
,
(1)求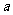 及
及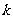 的值;
的值;
(2)求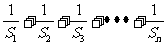 .
.
19.(本题满分12分)
㈠(重点班必答)
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立)
(1)求三人同时上网的概率;
(2)至少有几人同时上网的概率小于0.3 ?
㈡(平行班必答)
大西洋鲑鱼每年都要逆流而上2000km游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数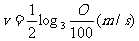 ,其中
,其中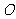 表示鱼的耗氧量的单位数.
表示鱼的耗氧量的单位数.
(1)求一条鱼静止时耗氧量的单位数;
(2)当一条鱼的耗氧量是8100个单位时它的游速是多少?
18.(本题满分12分)
如图,在直棱柱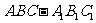 中,
中,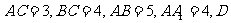 是
是 的中点:
的中点:
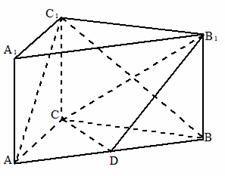
(1)求证: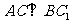
(2)求证: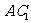 ∥平面
∥平面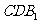
(3)求异面直线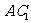 与
与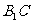 所成的角的余弦值.
所成的角的余弦值.
17.(本题满分12分)
已知 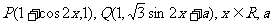 是常数,且函数
是常数,且函数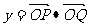 (
(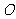 是坐标原点)
是坐标原点)
(1)求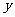 关于
关于 的函数关系式
的函数关系式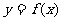 ;
;
(2)若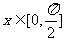 时,
时,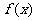 的最大值为4,求
的最大值为4,求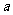 的值,并说明此时
的值,并说明此时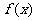 的图像可由
的图像可由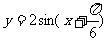 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
16.已知向量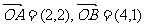 ,
,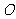 为坐标原点,在
为坐标原点,在 轴上找一点
轴上找一点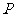 ,使
,使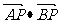 有最小值,则点
有最小值,则点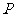 的坐标是
__________.
的坐标是
__________.
15.设函数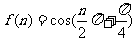 ,则
,则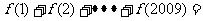 __________.
__________.
14.若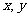 满足条件
满足条件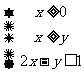 ,则
,则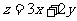 的最大值是 __________.
的最大值是 __________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com