
2.已知集合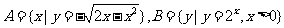 ,R是实数集,则
,R是实数集,则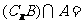
( )
A.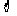 B.R
B.R
C.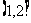 D.
D.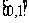
1.复数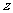 满足方程:
满足方程: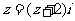 ,则
,则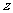 = ( )
= ( )
A.  B.
B.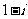 C.
C.
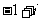 D.
D.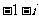
22.(从下面2个小题中任选一个作答)
(1)如图:在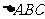 中,CD是AB边上的高,且
中,CD是AB边上的高,且 CAD=60°,求证:2BD=2AB-AC
CAD=60°,求证:2BD=2AB-AC
(2)已知曲线C的参数方程为 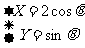 (θ为参数),曲线L的极坐标方程
(θ为参数),曲线L的极坐标方程
为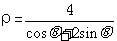 。
。
①判断曲线C与曲线L的位置关系。
②求曲线C的对称中心到曲线L的距离。
21.从椭圆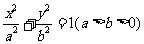 上一点P向
上一点P向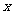 轴作垂线,垂足为左焦点
轴作垂线,垂足为左焦点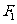 .又点
.又点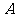 是椭圆与
是椭圆与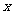 轴正半轴的交点,点
轴正半轴的交点,点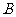 是椭圆与
是椭圆与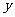 轴正半轴的交点,且
轴正半轴的交点,且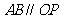 ,
,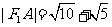 ,求椭圆的方程.
,求椭圆的方程.
20.已知函数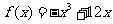 ,
,
①求函数的单调区间;
②求函数的极值,并画出函数的草图;
③当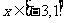 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.
19.(本小题满分13分)已知四棱锥P-ABCD的底面是边长为4的正方形,
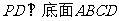 ,PD=6,M、N分别是PB、AB的中点;
,PD=6,M、N分别是PB、AB的中点;
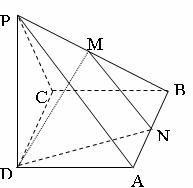
①求证: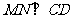
②求三棱锥P-DMN的体积。
18.选采问题:学校餐厅每天供应500名学生用餐,每星期一有A,B两种菜可供选择.调查资料表明,凡是在星期一选A种菜的,下星期一会有20% 改选B种菜;而选B种菜的,下星期一会有30% 改选A种菜.用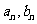 分别表示在第
分别表示在第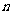 个星期选A的人数和选B的人数,如果
个星期选A的人数和选B的人数,如果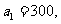 求
求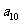 .
.
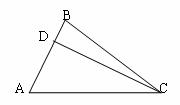
17.一次机器人足球比赛中,甲队1号机器人由点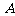 开始作匀速直线运动,到达点
开始作匀速直线运动,到达点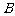 时,发现足球在点
时,发现足球在点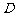 处正以2倍于自己的速度向点
处正以2倍于自己的速度向点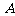 作匀速直线滚动.如图所示,已知
作匀速直线滚动.如图所示,已知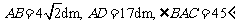 .若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
.若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?

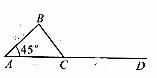
16.有以下四种变换方式:
①向左平行移动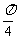 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的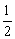 ;
;
②向右平行移动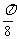 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的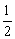 ;
;
③每个点的横坐标缩短为原来的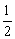 ,再向右平行移动
,再向右平行移动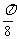 个单位长度;
个单位长度;
④每个点的横坐标缩短为原来的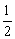 ,再向左平行移动
,再向左平行移动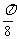 个单位长度
个单位长度
其中能将函数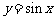 的图象变为函数
的图象变为函数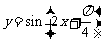 的图象的是___________
的图象的是___________
15.一个各项均正的等比数列,其每一项都等于它后面的相邻两项之和,则公比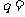 ________.
________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com