
20.(本小题共14分)
设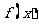 是定义在区间D上的函数,若对任何实数
是定义在区间D上的函数,若对任何实数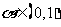 以及D中的任意两数
以及D中的任意两数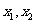 ,恒有
,恒有 ,则称
,则称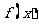 为定义在D上的C函数.
为定义在D上的C函数.
(Ⅰ)试判断函数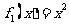 ,
,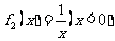 是否为各自定义域上的C函数,并说明理由;
是否为各自定义域上的C函数,并说明理由;
(Ⅱ)已知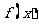 是R上的C函数,m是给定的正整数,设
是R上的C函数,m是给定的正整数,设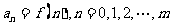 ,且
,且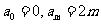 ,记
,记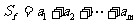 . 对于满足条件的任意函数
. 对于满足条件的任意函数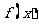 ,试求
,试求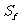 的最大值;
的最大值;
(Ⅲ)若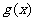 是定义域为R的函数,且最小正周期为T,试证明
是定义域为R的函数,且最小正周期为T,试证明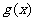 不是R上的C函数.
不是R上的C函数.
19.(本小题共14分)
设函数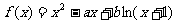
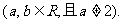 .
.
(Ⅰ)当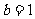 且函数
且函数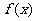 在其定义域上为增函数时,求
在其定义域上为增函数时,求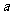 的取值范围;
的取值范围;
(Ⅱ)若函数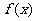 在
在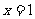 处取得极值,试用
处取得极值,试用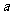 表示
表示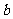 ;
;
(Ⅲ)在(Ⅱ)的条件下,讨论函数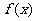 的单调性.
的单调性.
18.(本小题共14分)
某中学已选派20名学生观看当地举行的三场(同时进行)比赛,名额分配如下:
|
足球 |
跳水 |
柔道 |
|
10 |
6 |
4 |
(Ⅰ)从观看比赛的学生中任选2名,求他们观看的恰好是同一场比赛的概率;
(Ⅱ)从观看比赛的学生中,任选3人,求他们中至少有1人观看的是足球比赛的概率;
(Ⅲ) 如果该中学可以再安排4名教师选择观看上述3场比赛(假设每名教师选择观看各场比赛是等可能的,且各位教师的选择是相互独立的),记观看足球比赛的教师人数为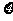 ,求随机变量
,求随机变量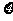 的分布列和数学期望.
的分布列和数学期望.
17.(本小题共13分)
设数列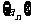 的前
的前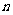 项和为
项和为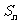 ,且满足
,且满足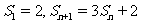
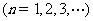 .
.
(Ⅰ)证明数列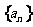 是等比数列并求通项
是等比数列并求通项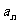 ;
;
(Ⅱ)求数列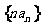 的前
的前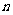 项和
项和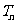 .
.
16.(本小题共13分)
已知函数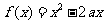 ,把函数
,把函数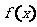 的图象向左平移一个单位得到函数
的图象向左平移一个单位得到函数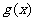 的图象,且
的图象,且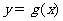 是偶函数.
是偶函数.
(Ⅰ)求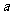 的值;
的值;
(Ⅱ)设函数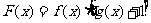 ,求函数
,求函数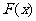 在区间
在区间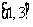 上的最大值和最小值.
上的最大值和最小值.
15.(本小题共12分)
已知关于x的不等式组 ,其中
,其中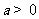 .
.
(Ⅰ)求不等式①的解集;
(Ⅱ)若不等式组的解集为空集,求实数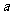 的取值范围.
的取值范围.
14.定义在实数集R上的函数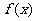 ,如果存在函数
,如果存在函数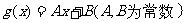 ,使得
,使得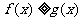 对一切实数
对一切实数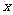 都成立,那么称
都成立,那么称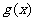 为函数
为函数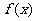 的一个承托函数. 下列说法正确的有: .(写出所有正确说法的序号)
的一个承托函数. 下列说法正确的有: .(写出所有正确说法的序号)
①对给定的函数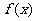 ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个;
②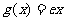 为函数
为函数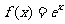 的一个承托函数;
的一个承托函数;
③函数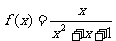 不存在承托函数;
不存在承托函数;
④函数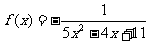 ,若函数
,若函数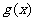 的图象恰为
的图象恰为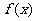 在点
在点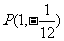 处的切线,则
处的切线,则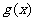 为函数
为函数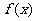 的一个承托函数.
的一个承托函数.
13.设甲、乙两人每次射击命中目标的概率分别为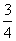 和
和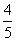 ,且各次射击相互独立.若甲、乙各射击一次,则甲命中但乙未命中目标的概率是_________;若按甲、乙、甲…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时甲射击了两次的概率是_________.
,且各次射击相互独立.若甲、乙各射击一次,则甲命中但乙未命中目标的概率是_________;若按甲、乙、甲…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时甲射击了两次的概率是_________.
12.已知等差数列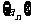 中,
中,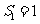 ,
,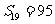 ,那么
,那么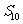 = ___________.
= ___________.
11.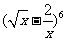 的展开式中常数项是
. (用数字作答)
的展开式中常数项是
. (用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com