
19.(本小题满分12分)
如图,在四棱锥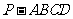 中,底面
中,底面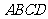 为正方形,且
为正方形,且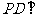 平面
平面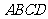 ,
,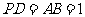 ,
,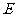 、
、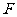 分别是
分别是 、
、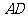 的中点.
的中点.
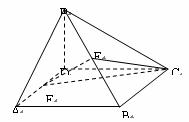
(Ⅰ)证明: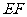 ∥平面
∥平面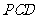 ;
;
(Ⅱ)求二面角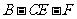 的大小.
的大小.
18.(本小题满分12分)
已知甲、乙两名射击运动员各自独立地射击1次,命中10环的概率分别为 、
、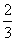 ;
;
(Ⅰ)求乙在第3次射击时(每次射击相互独立)才首次命中10环的概率;
(Ⅱ)若甲、乙两名运动员各自独立地射击1次,求两人中恰有一人命中10环的概率.
17.(本小题满分12分)
已知函数 ,,
,,
(Ⅰ)求函数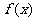 的最小正周期、最大值及取得最大值时自变量
的最小正周期、最大值及取得最大值时自变量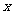 的集合;
的集合;
(Ⅱ)设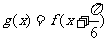 ,试判断函数
,试判断函数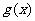 的奇偶性.
的奇偶性.
16.给定下列命题:
①半径为2,圆心角的弧度数为 的扇形的面积为
的扇形的面积为 ;
;
②若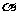 、
、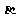 为锐角,
为锐角, ,
,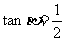 ,则
,则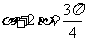 ;
;
③若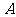 、
、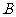 是△
是△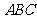 的两个内角,且
的两个内角,且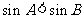 ,则
,则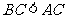 ;
;
④若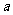 、
、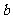 、
、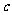 分别是△
分别是△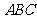 的三个内角
的三个内角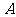 、
、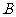 、
、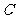 所对边的长,
所对边的长,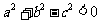 ,则△
,则△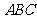 一定是钝角三角形.其中真命题的序号是
.
一定是钝角三角形.其中真命题的序号是
.
15.设实数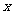 、
、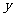 满足约束条件,
满足约束条件,  ,则z=3x+y的最大值是 。
,则z=3x+y的最大值是 。
14.若向量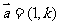 ,
,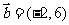 ,
,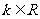 ,且
,且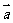 ∥
∥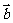 ,则
,则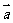

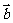 = .
= .
13.若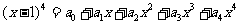 ,则
,则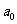 =
.
=
.
12.已知集合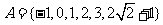 ,
,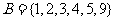 ,映射
,映射 的对应法则为
的对应法则为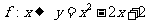 .设集合
.设集合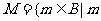 在集合
在集合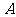 中存在原象
中存在原象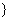 ,集合
,集合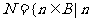 在集合
在集合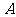 中不存在原象
中不存在原象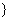 ,若从集合
,若从集合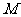 、
、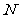 中各取一个元素组成没有重复数字的两位数的个数 ( )
中各取一个元素组成没有重复数字的两位数的个数 ( )
A.60 B.44 C.20 D.12
|
11.设双曲线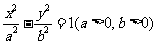 的左、右焦点分别是
的左、右焦点分别是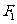 、
、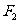 ,过点
,过点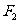 的直线交双曲线右支于不同的两点
的直线交双曲线右支于不同的两点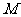 、
、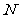 .若△
.若△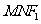 为正三角形,则该双曲线的离心率为( )
为正三角形,则该双曲线的离心率为( )
A.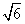 B.
B.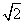 C.
C.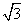 D.
D.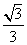
9.8名志愿者中,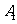 、
、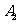 、
、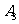 为教师,
为教师,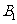 、
、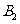 、
、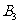 、
、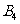 为医生,
为医生,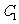 、
、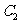 为学生.为组建一个服务小组,需从这9名志愿者中选出教师1名、医生2名、学生1名,则
为学生.为组建一个服务小组,需从这9名志愿者中选出教师1名、医生2名、学生1名,则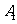 被选中且
被选中且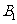 、
、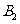 最多有1名被选中的概率为 ( )
最多有1名被选中的概率为 ( )
A.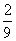 B.
B.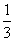 C.
C.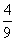 D.
D.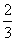
|
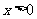 ,
,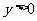 ,
,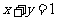 ,则
,则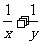 的最小值是 ( )
的最小值是 ( )
A.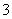 B.
B.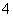 C.
C.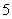 D.6
D.6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com