
8.设向量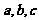 ,满足
,满足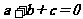 ,且
,且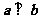 ,
,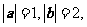 则
则 = ( )
= ( )
A.1 B.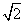 C.2 D.
C.2 D.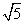
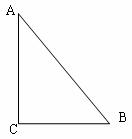
7.如右图所示,已知△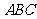 是等腰直角三角形,
是等腰直角三角形,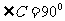 ,
,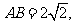 则
则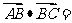
A.4 B. C.2 D.
C.2 D.
6.给出命题:已知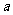 、
、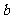 为实数,若
为实数,若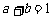 ,则
,则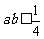 .在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( )
.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( )
A.3 B.2 C.1 D.0
5.设向量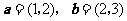 ,若向量
,若向量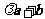 与向量
与向量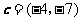 共线,则
共线,则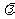 的值为( )
的值为( )
A.1 B.2 C.3 D.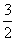
4.在△ABC中“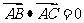 ”是“△ABC为直角三角形”的 ( )
”是“△ABC为直角三角形”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.命题“对任意的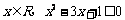 ”的否定是 ( )
”的否定是 ( )
A.存在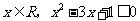 B.存在
B.存在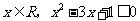
C.存在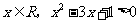 D.对任意的
D.对任意的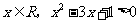
2.已知复数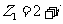 ,
,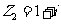 ,则
,则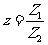 在复平面内的对应点位于 ( )
在复平面内的对应点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.已知集合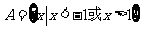 ,
,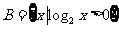 ,则
,则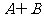 = ( )
= ( )
A.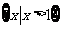 B.
B.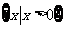 C.
C.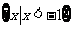 D.
D.
22.(本题满分14分)
已知函数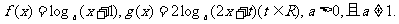
(1)若1是关于x的方程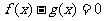 的一个解,求t的值;
的一个解,求t的值;
(2)当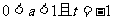 时,解不等式
时,解不等式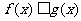 ;
;
(3)若函数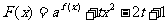 在区间
在区间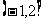 上有零点,求t的取值范围.
上有零点,求t的取值范围.
附加题:(本题解答正确完整给10分,不答或答错不扣分,只有结论没有过程不给分)
设函数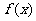 定义域为R,当x<0时,f(x)>1,且对于任意的x∈R,有f(x + y)=f(x)•f(y)成立.数列{an}满足a1=f(0),且f(
定义域为R,当x<0时,f(x)>1,且对于任意的x∈R,有f(x + y)=f(x)•f(y)成立.数列{an}满足a1=f(0),且f(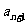 )=
)=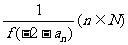 .问:是否存在正数k,使(1+
.问:是否存在正数k,使(1+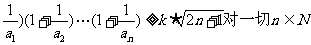 均成立,若存在,求出k的最大值并证明,否则说明理由.
均成立,若存在,求出k的最大值并证明,否则说明理由.
21.(本题满分12分)
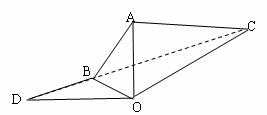
如图,海岛O上有一座海拔1千米的山,山顶上设有一个观察站A(即OA=1千米且OA⊥平面COB),上午11时测得一轮船在岛北偏东60º的C处,俯角为30º,11时10分又测得该船在岛北偏西60º的B处,俯角为60º.
(1)该船的速度为每小时多少千米?
(2)若该船不改变航向继续前进到D处,测得∠CDO的正弦值为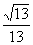 ,问此时D O的距离为多少千米?
,问此时D O的距离为多少千米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com