
6.已知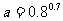 ,
,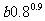 ,
,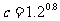 ,则的大小关系是
,则的大小关系是
A.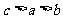 B.
B.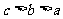 C.
C.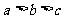 D.
D.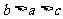
5.设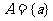 ,则下列各式一定正确的是
,则下列各式一定正确的是
A.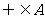 B.
B.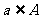 C.
C.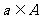 D.
D.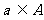
4.已知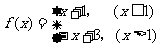 ,则
,则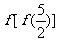 的值为
的值为
A.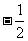 B.
B.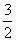 C.
C.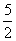 D.
D.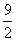
3.已知 ,
,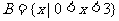 ,则
,则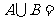
A.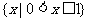 B.
B.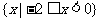
C.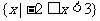 D.
D.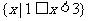
2.若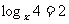 ,则
,则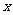 的值为
的值为
A.±2 B.2
C.-2 D.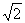
1.设全集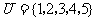 ,
,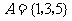 ,
,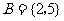 ,则
,则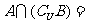
A.{2} B.{2,3} C.{3} D.{1,3}
21.(本小题满分13分)
已知数列{an}满足条件a1=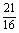 ,2an-3an-1=
,2an-3an-1=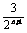 ,n≥2.
,n≥2.
(1)求数列{an}的通项公式;
(2)已知m为正整数,当2≤n≤m时,证明:(an+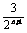 )
)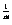 ≤
≤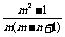 ;
;
(3)已知当正整数m≥2时,有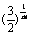 <1+
<1+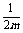 .试利用该结论证明:当1≤n≤m,m≥2 时,有:(an+
.试利用该结论证明:当1≤n≤m,m≥2 时,有:(an+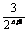 )
)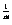 [m-
[m-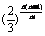 ]<
]<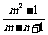 .
.
20.(本小题满分13分)
当兔子和狐狸处于同一栖息地时,忽略其他因素,只考虑兔子数量和狐狸数量的相互影响,为了简便起见,不妨做如下假设:①由于自然繁殖,兔子数每年增长10%,狐狸数每年减少15%;②由于狐狸吃兔子,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍;③第n年的年初时,兔子数量用Rn表示,狐狸数量用Fn表示;④初始时刻(即第1年的年初),兔子数量有R1=100,狐狸数量有F1=30.请用所学知识解决如下问题:
(1)列出兔子与狐狸的生态模型(即Rn、Fn的关系式);
(2)分别求出Rn、Fn关于n的关系式;
(3)讨论当n越来越大时,兔子与狐狸的数量是否能达到一个稳定的平衡状态,说明你的理由.
19.(本小题满分13分)
已知0<α<β<π.
(1)求证: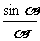 >
>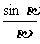 ;
;
(2)在△ABC中,已知∠A、∠B、∠C的对边分别为a、b、c,当∠B=2∠A时,判断6a、3b、2c的大小,并说明理由.
18.(本小题满分12分)
已知数列{an}的前n项之和Sn与an满足关系式:nSn+1=(n+2)Sn+an+2(n∈N*).
(1)若a1=0,求a2,a3的值;
(2)求证:a1=0是数列{an}为等差数列的充要条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com