
7.已知a>0,f(x)=ax3+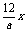 且f′(1) ≤12,则实数a=
且f′(1) ≤12,则实数a=
A.4 B.3 C.2 D.1
6.已知a、b、c∈R,则下列推理:
①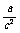 >
>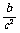
 a>b
②a3>b3,ab>0
a>b
②a3>b3,ab>0
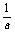 <
<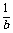
③a2>b2,ab>0
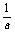 <
<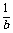 ④0<a<b<1
④0<a<b<1 loga(1+a) >logb
loga(1+a) >logb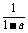
其中正确的个数是
A.1 B.2 C.3 D.4
5.已知命题p:函数f(x)=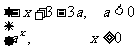 (a>0且a≠1)是(-∞,+∞)上的减函数;命题q:a∈(0,
(a>0且a≠1)是(-∞,+∞)上的减函数;命题q:a∈(0,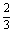 ).则p是q的
).则p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.当0≤x≤π时,函数f(x)=sinx+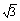 cosx的
cosx的
A.最大值是2,最小值是-1
B.最大值是1 ,最小值是-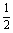
C.最大值是2,最小值是-2
D.最大值是2,最小值是-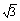
3.在等差数列{an}中,a3+a7-a10=8,a11-a4=4,则S13等于
A.152 B.154 C.156 D.158
2.已知函数y=Asin(ωx+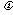 )(A>0,ω>0,|
)(A>0,ω>0,|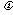 |<
|<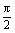 ) 的图象如图所示,则
) 的图象如图所示,则
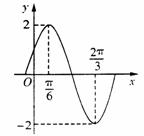
A.y=2sin(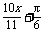 )
B.y=2sin(
)
B.y=2sin(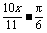 )
)
C.y=2sin(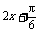 )
D.y=2sin(
)
D.y=2sin(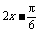 )
)
1.设集合A={x|y=ln(1-x)},集合B={y|y=x2},则A∩B=
A.[0,1] B.[0,1) C.(-∞,1] D.(-∞,1)
21. (本小题满分13分)
数列{an}中a1=t,a2=t2(t>0且t≠1). x=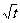 是函数f(x)=an-1 x3-3[(t+1)an-an+1 ] x+1(n≥2)的一个极值点.
是函数f(x)=an-1 x3-3[(t+1)an-an+1 ] x+1(n≥2)的一个极值点.
(1)证明数列{ an-1-an}是等比数列,并求数列{an}的通项公式;
(2)记bn=2(1-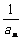 ),当t=2时,数列{bn}的前几n项和为Sn,求使Sn>2008的n 的最小值;
),当t=2时,数列{bn}的前几n项和为Sn,求使Sn>2008的n 的最小值;
(3)当t=2时,是否存在指数函数g(x),使得对于任意的正整数n有
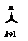
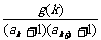 <
<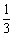 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由(说明:
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由(说明: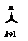 f(k)=f(1)+f(2)+…+f(n).
f(k)=f(1)+f(2)+…+f(n).
20. (本小题满分13分)
已知定义在R上的函数f(x)满足:f(x+y)=f(x)+f(y),当x<0时,
f(x)<0.
(1)求证:f(x)在R上是增函数;
(2)解关于x的不等式:f(mx2)-2f(x)>f(m2x)-2f(m)(m>0,且m为常数).
19. (本小题满分13分)
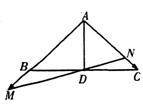
D是三角形ABC中BC边的中点,过点D作直线分别交直线AB、AC于点M、N,设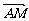 =m
=m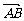 ,
,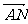 =n
=n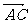 ,
,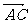 =a,
=a,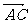 =b. 且m>0,n>0.
=b. 且m>0,n>0.
(1)分别用向量a、b表示向量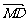 和
和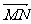 ;
;
(2)求证: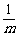 +
+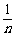 是定值;
是定值;
(3)求m+n的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com