
1.△ABC中,AB=1,BC=2,则∠C的范围是 ( )
A.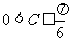 B.
B.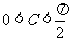
C.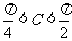 D.
D.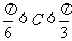
22.(14分)设函数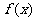 的定义域是R,对于任意实数
的定义域是R,对于任意实数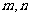 ,恒有
,恒有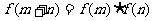 ,且当
,且当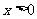 时,
时,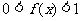 .
.
(1)求证: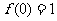 ,且当
,且当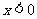 时,有
时,有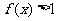 ;
;
(2)判断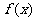 在R上的单调性;
在R上的单调性;
(3)设集合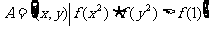 ,集合
,集合 ,若
,若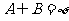 ,求
,求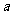 的取值范围.
的取值范围.
21.(12分)某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
|
消费金额(元)的范围 |
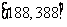 |
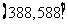 |
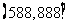 |
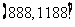 |
…… |
|
获得奖券的金额(元) |
28 |
58 |
88 |
128 |
…… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为400元的商品,则消费金额为320元,然后还能获得对应的奖券金额为28元. 于是,该顾客获得的优惠额为: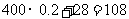 元. 设购买商品得到的优惠率=
元. 设购买商品得到的优惠率= .试问:
.试问:
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)当商品的标价为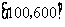 元时,试写出顾客得到的优惠率
元时,试写出顾客得到的优惠率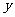 关于标价
关于标价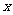 元之间的函数关系式;
元之间的函数关系式;
(3)当顾客购买标价不超过600元的商品时,该顾客是否可以得到超过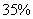 的优惠率?若可以,请举一例;若不可以,试说明你的理由.
的优惠率?若可以,请举一例;若不可以,试说明你的理由.
20.(12分)已知函数f ( x )=x 2+ax+b,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞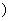 上是增函数.
上是增函数.
19.(12分)设关于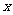 的函数
的函数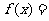
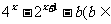 R),
R),
(1)若函数有零点,求实数b的取值范围;
(2)当函数有零点时,讨论零点的个数,并求出函数的零点.
18.(12分)设定义域为R的函数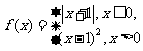 .
.
(1)在平面直角坐标系内作出该函数的图像;
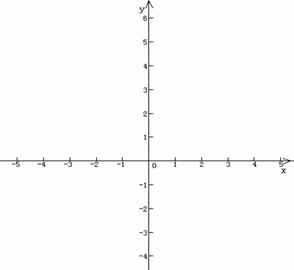
(2)试找出一组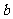 和
和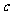 的值,使得关于
的值,使得关于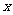 的方程
的方程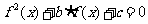 有7个不同的实根.请说明你的理由.
有7个不同的实根.请说明你的理由.
17.(12分)已知M={1,2,a2-3a-1 },N={-1,a,3},M∩N={3},求实数a的值.
16.2007年10月27日全国人大通过了关于修改个所得税的决定,工薪所得减去费用标准从800元提高到1600元,也就是说原来月收入超过800元部分就要纳税,2008年1月1日开始超过1600元才纳税,若税法修改前后超过部分的税率相同,如下表:
|
级数 |
全月应纳税所得额 |
税率(%) |
|
1 |
不超过500元 |
5 |
|
2 |
500~2000元 |
10 |
|
3 |
2000~5000元 |
15 |
某人2008年6月交纳个人所得税123元,则按照新税法只要交___________元.
15.若函数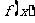 既是幂函数又是反比例函数,则这个函数是
既是幂函数又是反比例函数,则这个函数是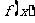 =
.
=
.
14.一元二次方程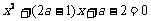 的一根比1大,另一根比-1小,则实数a的取值范围是
.
的一根比1大,另一根比-1小,则实数a的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com