
7.若函数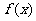 是偶函数,且当
是偶函数,且当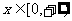 时,
时,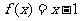 ,则不等式
,则不等式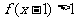 的解集是( )
的解集是( )
A.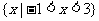 B.
B.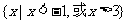 C.
C.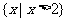 D.
D.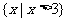
6.若定义在区间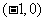 内的函数
内的函数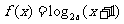 满足
满足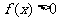 ,则实数
,则实数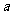 的取值范围是( )
的取值范围是( )
A.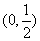 B.
B.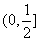 C.
C.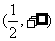 D.
D.
5.函数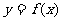 的反函数
的反函数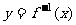 的图象与
的图象与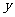 轴交于点
轴交于点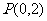 ,则方程
,则方程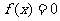 的根是
的根是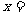 ( )
( )
A.4 B.3 C.2 D.1
4.根据下表中的数据,可以判定方程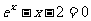 的一个根所在的区间是( )
的一个根所在的区间是( )
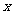 |
-1 |
0 |
1 |
2 |
3 |
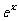 |
0.37 |
1 |
2.72 |
7.39 |
20.0 |
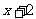 |
1 |
2 |
3 |
4 |
5 |
A.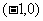 B.
B.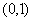 C.
C.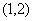 D.
D.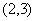
3.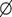 已知集合
已知集合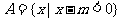 ,
,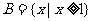 ,则
,则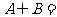 的一个必要而不充分条件为( )
的一个必要而不充分条件为( )
A.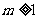 B.
B. 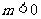 C.
C. 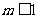 D.
D.
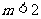
2.函数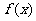 =
=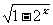 的定义域是( )
的定义域是( )
A. B.
B.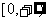 C.
C. D.
D.
1.若复合命题“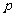 且
且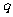 ”,“
”,“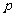 或
或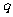 ”仅有一个为真,则(
)
”仅有一个为真,则(
)
A.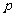 、
、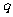 都为真 B.
都为真 B.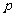 、
、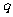 都为假 C.
都为假 C.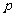 、
、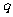 一真一假 D.不能判断
一真一假 D.不能判断
22、f(x)=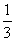 ax3+bx2+cx+d,其中a、b、c、是以d为公差的等差数列,且a>0,d>0,设x0为f(x)的极小值点。在[1-
ax3+bx2+cx+d,其中a、b、c、是以d为公差的等差数列,且a>0,d>0,设x0为f(x)的极小值点。在[1-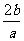 ,0]上,f /(x)在x1处取最大值,在x2处取最小值,记点A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
,0]上,f /(x)在x1处取最大值,在x2处取最小值,记点A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
(1)求x0的值;
(2)若△ABC有一条边平行于x轴,且面积为2+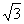 ,求a、d的值。
(14分)
,求a、d的值。
(14分)
21、{an}为等差数列,且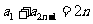 ,
,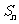 为数列{
为数列{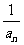 }的前n项和,设
}的前n项和,设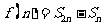
(1)比较f(n)与f(n+1)的大小;
(2)若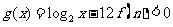 ,在x∈[a,b]且对任意n>1,n∈N*恒成立,求实数a、b满足的条件。
(12分)
,在x∈[a,b]且对任意n>1,n∈N*恒成立,求实数a、b满足的条件。
(12分)
20、函数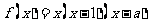 (a>1)
(a>1)
(1)证明:函数f(x)有两个不同的极值点x1、x2;
(2)若不等式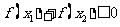 成立,求a的范围。
(12分)
成立,求a的范围。
(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com