
22.(本小题满分12分)
双曲线C的对称中心在坐标原点,顶点A1,A2(A2为右顶点)在χ轴上,离心率为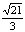 且经过点P(6,6),动直线L经过△A1PA2的重心G与双曲线C交于M、N两点,R为线段MN中心,
且经过点P(6,6),动直线L经过△A1PA2的重心G与双曲线C交于M、N两点,R为线段MN中心,
(Ⅰ)求双曲线C的标准议程;
(Ⅱ)当直线L的斜率为何值时,RA2⊥PA2。
21.(本小题满分12分)
设函数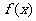 是奇数,当
是奇数,当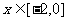 时,
时,
(Ⅰ)若 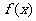 在
在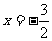 处有极值,求a值;
处有极值,求a值;
(Ⅱ)求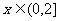 时,
时,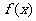 的解析式;
的解析式;
(Ⅲ)若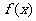 在
在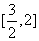 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
20.(本小题满分12分)
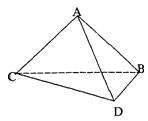
如图,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6,
(Ⅰ)求证:平面ABD⊥平面ACD;
(Ⅱ)求二面角A-CD-B的平面角的正切值.
19.(本小题满分12分)
某售货员负责在甲、乙、丙三个柜面上售货,如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7,假定各柜面是否需要照顾相互之间没有影响,求在这个小时内:
(Ⅰ)只有丙柜面需要售货员照顾的概率;
(Ⅱ)三个柜面最多有一个需要售货员照顾的概率.
18.(本小题满分12分)
已知函数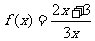 ,数列{an}的首项a1=1,an+1=
,数列{an}的首项a1=1,an+1=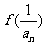 ,它的前n项和为Sn,
,它的前n项和为Sn,
(Ⅰ)求Sn的表达式;
(Ⅱ)若数列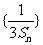 的前n项和为Tn.
的前n项和为Tn.
17.(本小题满分10分)
在△ABC中,角A、B、C所对的边分别为a、b、c向量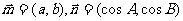 若
若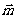 ∥
∥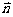 ,
,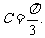
(Ⅰ)求角A、B的值;
(Ⅱ)若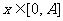 ,求函数
,求函数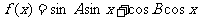 的最大值及最小值.
的最大值及最小值.
16.抛物线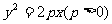 的动弦AB长为a(a>2p),则动弦AB的中点M到y轴的最短距离是
.
的动弦AB长为a(a>2p),则动弦AB的中点M到y轴的最短距离是
.
15.已知正四棱锥S-ABCD的高为4,侧棱与底面所成角为60°,则该正四棱锥的侧面与底面所成的角正切值是 .
14.若函数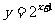 ,则
,则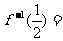 .
.
13.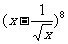 的展开式中χ5的系数为 .
的展开式中χ5的系数为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com