
22.(本小题满分14分)
已知椭圆 是抛物
是抛物
线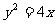 的一条切线.
的一条切线.
(I)求椭圆的方程;
(II)过点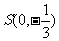 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
21.(本小题满分12分)
已知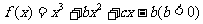 在[-1,0]和[0,2]上有相反的单调性.
在[-1,0]和[0,2]上有相反的单调性.
(I)求c的值;
(II)若函数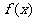 在[0,2]和[4,5]上有相反的单调性,
在[0,2]和[4,5]上有相反的单调性,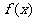 的图象上是否存在一点M,使得
的图象上是否存在一点M,使得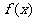 在点M的切线斜率是3b?若存在,求出M点坐标;若不存在,请说明理由;
在点M的切线斜率是3b?若存在,求出M点坐标;若不存在,请说明理由;
(III)若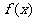 图象上有两点
图象上有两点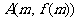 、
、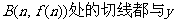 轴垂直,且函数
轴垂直,且函数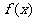 在区间[m,n]上存在零点,求实数b的取值范围.
在区间[m,n]上存在零点,求实数b的取值范围.
20.(本小题满分12分)
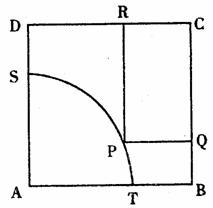
如图所示,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形草地,P是弧TS上一点,其余部分都是空地.现开发商想在空地上建造一个有两边分别落在BC和CD上的长方形停车场PQCR.
(I)设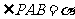 ,长方形PQCR的面积为S,试建立S关于α的函数关系式;
,长方形PQCR的面积为S,试建立S关于α的函数关系式;
(II)当α为多少时,S最大,并求最大值.
19.(本小题满分12分)
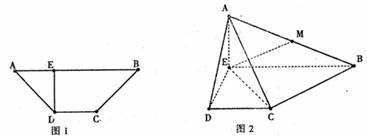
已知四边形ABCD是等腰梯形,AB=3,DC=1,∠BAD=45°,DE⊥AB(如图1)。现将△ADE沿DE折起,使得AE⊥EB(如图2),连结AC,AB,设M是AB的中点。
(I)求证:BC⊥平面AEC;
(II)判断直线EM是否平行于平面ACD,并说明理由.
18.(本小题满分12分)
已知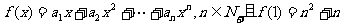 ,
,
(I)求数列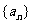 的通项公式;
的通项公式;
(II)设各项均为正数的等比数列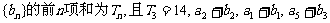 成等差数列,求Tn.
成等差数列,求Tn.
17.(本小题满分12分)
已知向量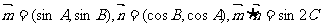 ,且A、B、C分别为△ABC的三边a、b、c所对的角。
,且A、B、C分别为△ABC的三边a、b、c所对的角。
(I)求角C的大小;
(II)若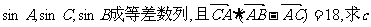 边的长。
边的长。
16.若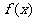 是定义在实数集R上的奇函数,且是周期为2的周期函数,当
是定义在实数集R上的奇函数,且是周期为2的周期函数,当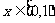 时,
时, 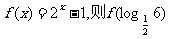 =
。
=
。
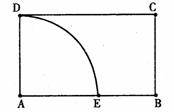
15.如图,四边形ABCD为矩形,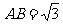 ,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率是 。
,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率是 。
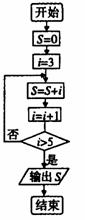
14.如图所示的程序框图,输出S的值为 。
13.数列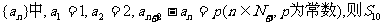 =
。
=
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com