
8.某科技小组有6名同学,现从中选出3人去参观展览,至少有1名女生入选时的不同选法有16种,则小组中的女生数目为 ( )
A.2 B.3 C.4 D.5
7.某种产品市场产、销量情况如图所示,其中: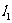 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;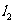 表示产品各年的销售情况.下列叙述:
表示产品各年的销售情况.下列叙述:
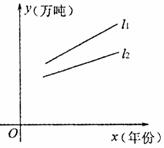
①产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
②产品已经出现了供大于求的情况,价格将趋跌;
③产品的库存积压将越来越严重,应压缩产量或扩大销售量;
④产品的产、销情况均以一定的年增长率递增.你认为较合理的是 ( )
A.①②③ B.①③④ C.②④ D.②③
6.设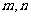 是两条不同的直线,
是两条不同的直线,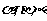 是三个两两不重合的平面,则
是三个两两不重合的平面,则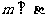 的一个充分条件是 ( )
的一个充分条件是 ( )
A.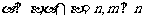 B.
B.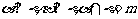
C.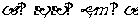 D.
D.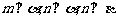
5.函数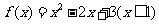 的反函数是 ( )
的反函数是 ( )
A.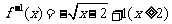 B.
B.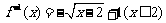
C.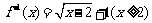 D.
D.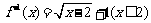
4.正项等差数列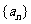 中,
中,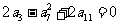 ,则
,则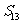 的值为 ( )
的值为 ( )
A.26 B.52 C.104 D.56
3.不等式组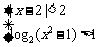 的解集为 ( )
的解集为 ( )
A.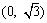 B.
B.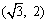 C.
C.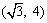 D.(2,4)
D.(2,4)
2.已知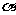 是第二象限的角,且
是第二象限的角,且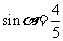 ,则
,则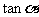 的值是 ( )
的值是 ( )
A.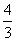 B.
B.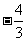 C.
C.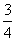 D.
D.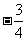
1.已知全集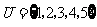 ,且
,且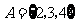 ,
,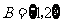 ,则
,则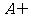 C
C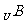 等于 ( )
等于 ( )
A.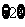 B.
B.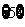 C.
C.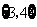 D.
D.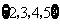
21.(本小题满分14分)
已知函数f(x)=ln(2+3x)-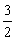 x2 .
x2 .
(1)求f(x)在[0, 1]上的极值;
(2)若对任意x∈[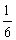 ,
,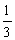 ],不等式|a-lnx|-ln[ f ’(x)+3x]>0成立,求实数a的取值范围;
],不等式|a-lnx|-ln[ f ’(x)+3x]>0成立,求实数a的取值范围;
(3)若关于x的方程f(x)=-2x+b在[0, 1]上恰有两个不同的实根,求实数b的取值范围.
20.(本小题满分12分)
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=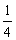 x2的焦点,离心率等于
x2的焦点,离心率等于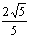 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若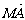 =λ1
=λ1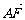 ,
,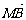 =λ2
=λ2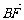 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com