
21.椭圆C的中心为坐标原点O,焦点在y轴上,离心率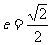 ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且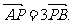
(1)求椭圆方程;
(2)求m的取值范围。
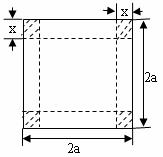
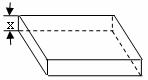
20.从边长2a的正方形铁片的四个角各截一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正常数t.
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.
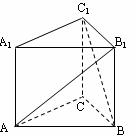
19.如图正三棱柱ABC-A1B1C1中,底面边长为a, 侧棱长为a。
(1)求二面角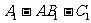 大小的余弦值;
大小的余弦值;
(2)在棱A1C1上确定一点D, 使BC1∥平面DAB1,说明理由.
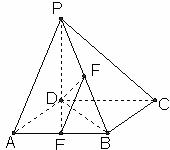
18.如图,在四棱椎P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点。
(1)求证:EF⊥CD;
(2)求DB与平面DEF所成角的正弦值。
17.已知函数f(x)=x3+ax2+bx+c在x=-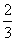 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值;
(2)若函数f(x)的图象与x轴有3个交点,求c的取值范围。
16.抛物线C的顶点在原点,焦点F与双曲线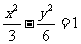 的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A、B两点。
的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A、B两点。
(1)求弦长|AB|;
(2)求弦AB中点到抛物线准线的距离。
15.若函数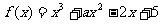 在区间(
在区间(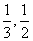 )上既不是单调递增函数,也不是单调递减函数,则实数a的取值范围是______________________.
)上既不是单调递增函数,也不是单调递减函数,则实数a的取值范围是______________________.
14.若椭圆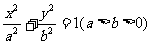 的左、右焦点分别为
的左、右焦点分别为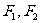 ,线段
,线段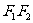 被抛物线
被抛物线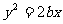 的焦点
的焦点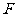 分成5﹕3的两段,则此椭圆的离心率为 .
分成5﹕3的两段,则此椭圆的离心率为 .
13.在平行六面体ABCD-A1B1C1D1中,AB = AD = AA1= 1,∠A1AB =∠A1AD =∠DAB
= 60°.则对角线AC1的长为 .
12.命题“若a=1, 则a2=1”的逆命题是______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com