
2.函数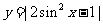 的最小正周期是
的最小正周期是
A.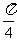 B.
B.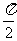 C.
C.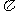 D.
D.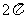
1.已知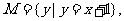
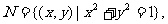 则集合
则集合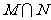 中元素的个数是
中元素的个数是
A.0 B.1 C.2 D.多个
20.(本小题满分14分)
已知函数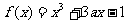 ,
,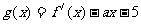 ,其中
,其中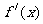 是
是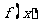 的导函数
的导函数
(Ⅰ)对满足 的一切
的一切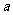 的值,都有
的值,都有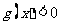 ,求实数
,求实数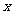 的取值范围;
的取值范围;
(Ⅱ)设 ,当实数
,当实数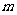 在什么范围内变化时,函数
在什么范围内变化时,函数 的图象与直线
的图象与直线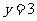 只有一个公共点
只有一个公共点
19.(本小题满分14分)已知二次函数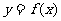 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为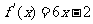 ,数列
,数列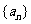 的前n项和为
的前n项和为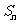 ,点
,点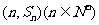 均在函数
均在函数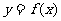 的图像上。
的图像上。
(Ⅰ)、求数列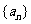 的通项公式;
的通项公式;
(Ⅱ)、设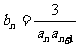 ,
,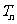 是数列
是数列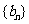 的前n项和,求使得
的前n项和,求使得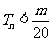 对所有
对所有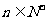 都成立的最小正整数m;
都成立的最小正整数m;
18.(本小题满分14分)设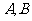 分别为椭圆
分别为椭圆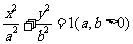 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且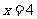 为它的右准线。
为它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设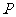 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线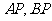 分别与椭圆相交于异于
分别与椭圆相交于异于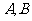 的点
的点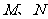 ,证明点
,证明点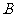 在以
在以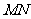 为直径的圆内。
为直径的圆内。
17.(本小题共 14 分) 如图,在底面为平行四边形的四棱锥 P-ABCD 中,AB⊥AC,PA⊥平面 ABCD,且 PA=PB,点 E 是 PD 的中点.
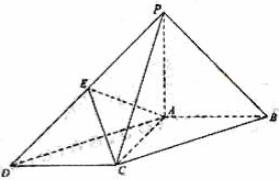 (Ⅰ)求证:AC⊥PB;
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB//平面 AEC;
16.(本小题满分12分)
甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
15.(本小题满分12分)
已知函数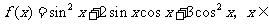
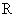 ,
,
求(1)函数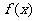 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量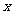 的集合;
的集合;
(2)函数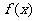 的单调增区间.
的单调增区间.
14.设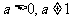 ,函数
,函数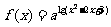 有最大值,则不等式
有最大值,则不等式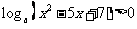 的解集为
。
的解集为
。
13.设A={1, 2, 3, 4, 5, 6},B={1, 3, 5, 7, 9}, 集合C是从A∪B中任取2个元素组成的集合,则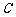
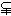
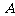 ∩
∩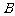 的概率是____________.
的概率是____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com