
5、设 ,则
,则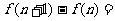 ( )
( )
A.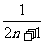 B.
B.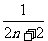 C.
C.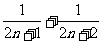 D.
D.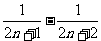
4、函数y=lg|x|( )
A.是偶函数,在区间(-∞,0)上单调递增
B.是偶函数,在区间(-∞,0)上单调递减
C.是奇函数,在区间(0,+∞)上单调递增
D.是奇函数,在区间(0,+∞)上单调递减
3、下述函数中,在 内为增函数的是 ( )
内为增函数的是 ( )
A.y=x2-2 B.y=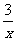 C.y=
C.y=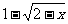 D.
D.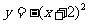
2、如图1-1,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是( )
A.(M∩P)∩S B.(M∩P)∪S
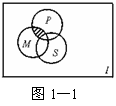 C.(M∩P)∩
C.(M∩P)∩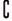 I S D.(M∩P)∪
I S D.(M∩P)∪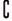 I S
I S
1、不等式组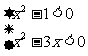 的解集是( )
的解集是( )
A.{x|-1<x<1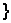 B.{x|0<x<3
B.{x|0<x<3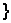 C.{x|0<x<1
C.{x|0<x<1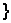 D.{x|-1<x<3}
D.{x|-1<x<3}
22、.(本小题14分) 设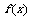 是定义在[-1,1]上的偶函数,,且当
是定义在[-1,1]上的偶函数,,且当
x∈[ -1,0 ] 时,f(x) = -2ax+4x3 .
(1)求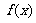 的解析式;
的解析式;
(2)若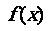 在
在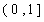 上为增函数,求
上为增函数,求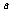 的取值范围;
的取值范围;
(3)是否存在正整数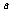 ,使
,使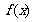 的图象的最高点落在直线
的图象的最高点落在直线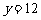 上?若存在,求出
上?若存在,求出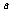 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
21、(本小题12分)已知函数: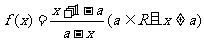 .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+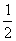 , a+1]时,求:f(x)的值域;
, a+1]时,求:f(x)的值域;
20、(本小题12分) 已知函数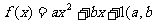 为实数),
为实数),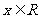 ,
,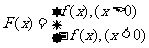
(Ⅰ)若f (-1) = 0,且函数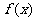 的值域为
的值域为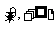 ,求
,求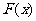 表达式;
表达式;
(Ⅱ)在(Ⅰ)的条件下,当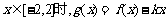 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
19、(本小题12分) 对某种赌博游戏调查后,发现其规则如下:摊主在口袋中装入8枚黑和8枚白的围棋子,参加者从中随意一次摸出5枚,摸一次交手续费1元,而中彩情况如下:
|
摸子情况 |
5枚白 |
4枚白 |
3枚白 |
其它 |
|
彩金 |
20元 |
2元 |
纪念品价值5角 |
无奖同乐一次 |
现在我们试计算如下问题:
(1)求一次获得20元彩金的概率;(结果用最简分数表示)
(2)分别求一次获2元和纪念奖的概率;(结果用最简分数表示)
(3)如果有1000次摸奖,摊主赔钱还是挣钱?是多少元?(精确到元)
18、(本小题12分) 设函数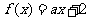 ,不等式
,不等式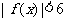 的解集为
的解集为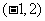 ,
,
试求不等式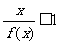 的解集
的解集
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com