
6. 已知数列{an}中,a1=8, a2 =4且满足an+1-2an+ an-1=0(n∈N*,n≥2),则数列{an}的前
30项的绝对值的和为( )
(A)870 (B)830 (C)1524 (D)1512
5. 当n∈N且n≥2时,1+2+22+…+24n-1=5p+q,其中p,q为非负整数,且0≤q<5,则q的值为 ( )
A.0 B.2 C.2 D.与n有关
4.已知l,m,表示直线,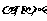 表示平面,下列条件中能推出结论的正确的是( )
表示平面,下列条件中能推出结论的正确的是( )
条件:①l⊥m,l⊥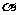 ,m⊥
,m⊥ ②
②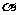 ∥
∥ ,
, ∥
∥ ③l⊥
③l⊥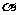 ,
,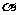 ∥
∥ ; ④ l⊥
; ④ l⊥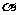 ,m⊥
,m⊥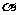
结论:a: l ⊥ b:
b: 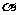 ⊥
⊥ c: l∥m d:
c: l∥m d: 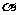 ∥
∥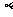
A ① a,②
a,② b,③
b,③ c,④
c,④ d
B ①
d
B ① b,②
b,② d,③
d,③ a,④
a,④ c
c
C ① c,②
c,② d,③
d,③ a,④
a,④ b
D ①
b
D ① d,②
d,② b,③
b,③ a,④
a,④ c
c
3. 已知函数y=f(n),(n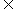 N*),如果7f(n)=f(n-1),f (1)=3,则
N*),如果7f(n)=f(n-1),f (1)=3,则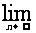 [f(1)+f(2)+…+f(n)]=( )
[f(1)+f(2)+…+f(n)]=( )
A.0 B.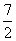 C.
C.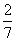 D.3
D.3
2.若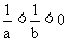 ,则下列结论不正确的是
( )
,则下列结论不正确的是
( )
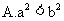
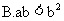
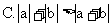
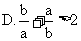
1.命题“若 ,则
,则 ”的否命题是
( )
”的否命题是
( )
A.若 ,则
,则 B.若
B.若 ,则
,则
C.若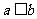 ,则
,则 D.若
D.若 ,则
,则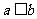
20、(16分)已知定义在R上的函数f(x),对任意的实数m、n,都有f(m+n)=f(m)f(n)成立,且对x>0时,
有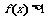 成立。
成立。
(1)证明:f(0)=1,且当x<0时,有: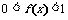 成立;
成立;
(2)证明:函数f(x)在R上为增函数;
(3)设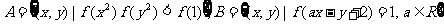 ,若
,若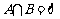 ,求实数
,求实数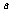 的取值范围。
的取值范围。
19、(14分)已知函数f(x)=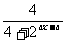 在[0,1]上的最小值为
在[0,1]上的最小值为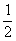 ,
,
(1)求f(x)的解析式; (2)若函数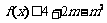 对
对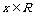 恒成立,求m的取值范围。
恒成立,求m的取值范围。
18、(14分) 已知函数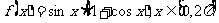 .
.
(1) 求函数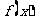 的单调区间;
(2) 求函数
的单调区间;
(2) 求函数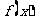 的最大值及最小值.
的最大值及最小值.
17、(14分)某运动员射击一次所得环数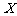 的分布如下:
的分布如下:
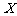 |
6 |
7 |
8 |
9 |
10 |
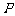 |
0 |
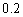 |
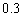 |
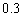 |
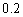 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为 .
.
(I)求该运动员两次都命中7环的概率; (II)求 的分布列; (Ⅲ) 求
的分布列; (Ⅲ) 求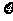 的数学期望。
的数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com