4.已知等差数列的第10项为23，第25项为－22，则此数列的通项公式为___________.

3.如果等差数列{a_n}的第5项为5，第10项为－5，那么此数列的第一个负数项是第________项.

2.在等差数列{a_n}中，若a₃+a₄+a₅+a₆+a₇=450，则a₂+a₈等于(　　 )

A.45　　　 　　 B.75　　　 C.180　　 D.300

1.首项为－24的等差数列，从第10项起开始为正数，则公差d的取值范围是　(　　 )

A.d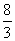＞　 B.d＜3 C. 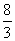≤d＜3 D.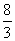＜d≤3

5．一个等差数列的第40项等于第20项与第30项的和，且公差是－10，试求首项和第10项．

[选修延伸]

[例4]等差数列{a_n}中，a₁=23，公差d为整数，若a₆>0,a₇<0.

(1)求公差d的值;

(2)求通项a_n.

[解]

[例5]甲、乙两人连续6年对某县农村养鸡业规模进行调查，提供两个不同的信息图如图所示．甲调查表明:从第1年每个养鸡场出产1万只鸡上升到第6年平均每个鸡场出产2万只鸡．乙调查表明:由第1年养鸡场个数30个减少到第6年10个．

请您根据提供的信息说明：

⑴第2年养鸡场的个数及全县出产鸡的总只数；

⑵到第6年这个县的养鸡业比第1年是扩大了还是

缩小了？请说明理由；

⑶哪一年的规模最大？请说明理由．

[解]

[追踪训练二]：

4．全国统一鞋号中，成年男鞋有14种尺码，其中最小的尺码是23．5cm，各相邻两个尺码都相差0．5cm，其中最大的尺码是多少？

3．诺沃尔(Knowall)在1740年发现了一颗彗星，并推算出在1823年、1906年、1989年……人们都可以看到这颗彗星，即彗星每隔83年出现一次．

(1)从发现那次算起，彗星第8次出现是在哪一年？

(2)你认为这颗彗星在2500年会出现吗？为什么？

[解]

2.等差数列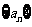中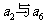，的等差中项为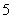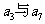，的等差中项为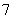，则______.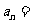

1．已知{a_n}是等差数列，a₇+a₁₃=20，则a₉+a₁₀+a₁₁=(　　 )

A.36　　 B.30　　　　　　 C.24　　 D.18

2．等差数列的单调性：由等差数列的定义知a_n+1－a_n=d,

当d＞0时，a_n+1____a_n即{a_n}为递增数列；

当d=0时，a_n+1_____a_n即{a_n}为常数列；

当d＜0时，a_n+1____a_n即{a_n}为递减数列.

注：等差数列不会是摆动数列.

[精典范例]

[例1]第一届现代奥运会于1986年在希腊雅典举行，此后每4年举行一次．奥运会如因故不能举行，届数照算．

(1)试写出由举行奥运会的年份构成的数列的通项公式；

(2)2008年北京奥运会是第几届？2050年举行奥运会吗？

[解]　　

[例2]在等差数列{a_n}中，

已知a₃＝10，a₉＝28，求a₁₂．

[解]

[例3]某滑轮组由直径成等差数列的6个滑轮组成．已知最小和最大的滑轮的直径分别为15cm和25cm，求中间四个滑轮的直径．

[解]

[追踪训练一]：