16. (本题满分14分)

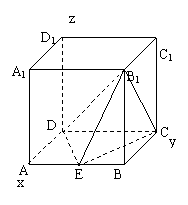
如图，在正方体ABCD-A₁B₁C₁D₁中，E为AB的中点.

(1)求直线B₁C与DE所成角的余弦值；

(2)求二面角E-B₁C-D的余弦值.(课本98页例4改编)

解：以DA、DC、DD₁所在的直线为x轴、y轴、z轴,

建立如图所示的直角坐标系，设正方体的棱长为a,则

D(0,0,0),E(a,0),C(0,a,0),B₁(a,a,a)　 ………………………2分

(1),,则

…………………7分

直线B₁C与DE所成角的余弦值为　　　　 ……………………………………8分

(2)，设平面B₁EC的法向量为，

则由得同理平面B₁DC的法向量

则　　　　　　　　　 ………………………………13分

所以求二面角E-B₁C-D的余弦值为　　 ……………………………………14分

15. (本题满分14分)

在ABC中，已知，，，求及.(课本16页第1题改编)

解：∵=cos

==_{……………………………………5分}

　　 ∴_{……………………………………7分}

求可以利用余弦定理，也可以利用正弦定理：

解法一：∵cos_{……………………12分}

　　 ∴_{…………………………………………14分}

解法二：∵sin_{………………………………10分}

又∵＞＜

∴＜，即＜＜∴_{………………………………………14分}

14. 如图，一条螺旋线是用以下方法画成：△ABC是边长为1的正三角形，曲线分别是以为圆心，为半径画的弧，曲线称为螺旋线，然后又以为圆心，为半径画弧……这样画到第圈，则所得螺旋线…，的总长度为.

13. 已知实数满足，则的最大值为 　4　 ．

12. 已知，若恒成立，则实数的取值范围是．

11．已知，则猜想的解析式为．

10. 求和：=-399. (课本第45页第2题原题)

9. 椭圆的焦点为F₁、F₂，过点F₁作直线与椭圆相交，被椭圆截得的最短的线段MN长为，的周长为20，则椭圆的离心率为．

8.用数学归纳法证明“”，从推导时原等式的左边应增加的项数是　 2^k　 ．

7.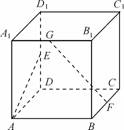如右图，在正方体中，E为棱中点、F为棱中点，G为棱上任意一点，则直线 AE与直线FG所成的角为 .(课本101页第7题改编)