
1.已知y=loga(2-ax)在 [0,1]上是x的减函数,则a的取值范围是
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
解析:∵y=loga(2-ax)在[0,1]上是关于x的减函数,
∴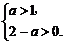 ∴1<a<2.
∴1<a<2.
答案:B
4.对于0≤m≤4的m,不等式x2+mx>4x+m-3恒成立,则x的取值范围是____________.
解析:转化为m(x-1)+x2-4x+3>0在0≤m≤4时恒成立.
令f(m)=m(x-1)+x2-4x+3.
则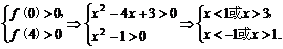
∴x<-1或x>3.
答案:x>3或x<-1
●典例剖析
[例1] 已知f(x)=loga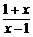 (a>0,a≠1).
(a>0,a≠1).
(1)判断f(x)在(1,+∞)上的单调性,并加以证明;
(2)当x∈(r,a-2)时,f(x)的值域为(1,+∞),求a与r的值;
(3)若f(x)≥loga2x,求x的取值范围.
剖析:单调性只要用定义证明,可先比较真数的大小再证.函数值域可利用函数的单调性确定端点后再比较,化为方程组求解.对数型不等式要化成同底后分a>1与0<a<1求解,同时要注意定义域.
解:(1)任取1<x1<x2,则
f(x2)-f(x1)=loga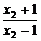 -loga
-loga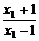
=loga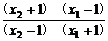
=loga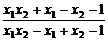 .
.
又∵x2>x1>1,∴x1-x2<x2-x1.
∴0<x1x2-x2+x1-1<x1x2-x1+x2-1.
∴0<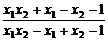 <1.
<1.
当a>1时,f(x2)-f(x1)<0,
∴f(x)在(1,+∞)上是减函数;
当0<a<1时,f(x2)-f(x1)>0,
∴f(x)在(1,+∞)上是增函数.
(2)由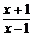 >0得x∈(-∞,-1)∪(1,+∞).
>0得x∈(-∞,-1)∪(1,+∞).
∵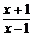 =1+
=1+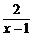 ≠1,∴f(x)≠0.
≠1,∴f(x)≠0.
当a>1时,
∵x>1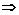 f(x)>0,x<-1
f(x)>0,x<-1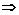 f(x)∈(0,1),
f(x)∈(0,1),
∴要使f(x)的值域是(1,+∞),只有x>1.
又∵f(x)在(1,+∞)上是减函数,
∴f-1(x)在(1,+∞)上也是减函数.
∴f(x)>1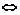 1<x<f-1(1)=
1<x<f-1(1)=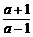 .
.
∴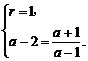 ∴
∴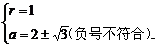
当0<a<1时,
∵x>1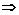 f(x)<0,x<1
f(x)<0,x<1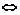 f(x)>0,
f(x)>0,
∴要使值域是(1,+∞),只有x<-1.
又∵f(x)在(-∞,-1)上是增函数,
∴f(x)>1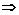 -1>x>f-1(1)=
-1>x>f-1(1)=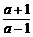 .
.
∴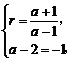 无解.
无解.
综上,得a=2+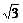 ,r=1.
,r=1.
(3)由f(x)≥loga2x得
当a>1时,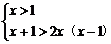
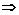
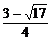 <x<
<x<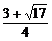 且x>1.
且x>1.
∴1<x<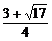 .
.
当0<a<1时,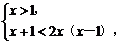
∴x>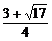 .
.
[例2] 已知抛物线y=ax2-1上存在关于直线x+y=0成轴对称的两点,试求实数a的取值范围.
解法一:设抛物线上关于直线l对称的两相异点为P(x1,y1)、Q(x2,y2),线段PQ的中点为M(x0,y0),设直线PQ的方程为y=x+b,由于P、Q两点存在,所以方程组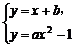 有两组不同的实数解,即得方程ax2-x-(1+b)=0. ①
有两组不同的实数解,即得方程ax2-x-(1+b)=0. ①
判别式Δ=1+4a(1+b)>0. ②
由①得x0=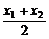 =
=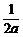 ,y0=x0+b=
,y0=x0+b=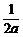 +b.
+b.
∵M∈l,∴0=x0+y0=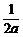 +
+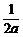 +b,
+b,
即b=-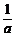 ,代入②解得a>
,代入②解得a>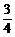 .
.
解法二:设同解法一,由题意得

将①②代入③④,并注意到a≠0,x1-x2≠0,得

由二元均值不等式易得
2(x12+x22)>(x1+x2)2(x1≠x2).
将⑤⑥代入上式得
2(-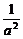 +
+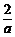 )>(
)>(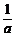 )2,解得a>
)2,解得a>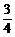 .
.
解法三:同解法二,由①-②,得
y1-y2=a(x1+x2)(x1-x2).
∵x1-x2≠0,∴a(x1+x2)=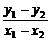 =1.
=1.
∴x0=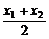 =
=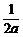 .∵M(x0,y0)∈l,
.∵M(x0,y0)∈l,
∴y0+x0=0,即y0=-x0=-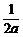 ,从而PQ的中点M的坐标为(
,从而PQ的中点M的坐标为(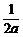 ,-
,-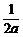 ).
).
∵M在抛物线内部,
∴a(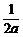 )2-(-
)2-(-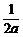 )-1<0.
)-1<0.
解得a>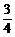 .(舍去a<0,为什么?)
.(舍去a<0,为什么?)
思考讨论
解法三中为何舍去a<0?
这是因为a<0,中点M(x0,y0),x0=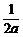 <0,
<0,
y0=-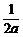 >0.又∵a<0,
>0.又∵a<0,
y=ax2-1<0,矛盾.∴a<0舍去.
●闯关训练
夯实基础
3.设M=a+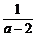 (2<a<3),N=log
(2<a<3),N=log (x2+
(x2+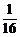 )(x∈R),那么M、N的大小关系是
)(x∈R),那么M、N的大小关系是
A.M>N B.M=N C.M<N D.不能确定
解析:由2<a<3,M=a+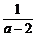 =(a-2)+
=(a-2)+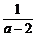 +2>2+2=4(注意a≠1,a≠3),
+2>2+2=4(注意a≠1,a≠3),
N=log (x2+
(x2+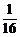 )≤log
)≤log
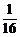 =4<M.
=4<M.
答案:A
2.(2004年福建,11)(理)定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则
A.f(sin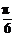 )<f(cos
)<f(cos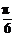 )
)
B.f(sin1)>f(cos1)
C.f(cos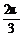 )<f(sin
)<f(sin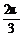 )
)
D.f(cos2)>f(sin2)
解析:由f(x)=f(x+2),知T=2,
又∵x∈[3,5]时,f(x)=2-|x-4|,可知当3≤x≤4时,f(x)=-2+x.
当4<x≤5时,f(x)=6-x.
其图象如下图.故在(-1,0)上是增函数,在(0,1)上是减函数.
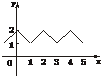
又由|cos2|<|sin2|,
∴f(cos2)>f(sin2).
答案:D
(文)定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4]时,f(x)=
x-2,则
A.f(sin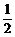 )<f(cos
)<f(cos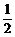 )
)
B.f(sin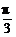 )>f(cos
)>f(cos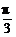 )
)
C.f(sin1)<f(cos1)
D.f(sin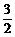 )>f(cos
)>f(cos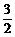 )
)
解析:仿理科分析.
答案:C
1.(2004年湖北,5)若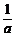 <
<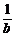 <0,则下列不等式中,正确的不等式有
<0,则下列不等式中,正确的不等式有
①a+b<ab ②|a|>|b| ③a<b
④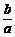 +
+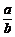 >2
>2
A.1个 B.2个 C.3个 D.4个
解析:∵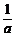 <
<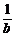 <0,∴b<a<0.
<0,∴b<a<0.
∴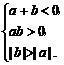 故①正确,②③错误.
故①正确,②③错误.
∵a、b同号且a≠b,∴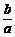 、
、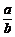 均为正.
均为正.
∴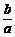 +
+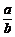 >2
>2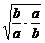 =2.
=2.
故④正确.∴正确的不等式有2个.
答案:B
2.解决上述问题的关键是找出综合题的各部分知识点及解法,充分利用数学思想和数学方法求解.
●点击双基
1.方程与不等式、函数与不等式、解析几何与不等式的综合问题.
6.7 不等式的综合问题
●知识梳理
3.与不等式相关联的知识较多,如函数与不等式、方程与不等式、数列与不等式、解析几何与不等式,要善于寻找它们之间的联系,从而达到综合应用的目的.
拓展例题
[例1] (2003年福建质量检测题)已知函数f(x)=|log2(x+1)|,实数m、n在其定义域内,且m<n,f(m)=f(n).
求证:(1)m+n>0;
(2)f(m2)<f(m+n)<f(n2).
(1)证法一:由f(m)=f(n),得|log2(m+1)|=|log2(n+1)|,即log2(m+1)=±log2(n+1),
log2(m+1)=log2(n+1), ①
或log2(m+1)=log2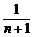 . ②
. ②
由①得m+1=n+1,与m<n矛盾,舍去.
由②得m+1=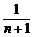 ,即(m+1)(n+1)=1. ③
,即(m+1)(n+1)=1. ③
∴m+1<1<n+1.∴m<0<n.∴mn<0.
由③得mn+m+n=0,m+n=-mn>0.
证法二:(同证法一得)(m+1)(n+1)=1.
∵0<m+1<n+1,∴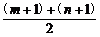 >
>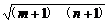 =1.∴m+n+2>2.∴m+n>0.
=1.∴m+n+2>2.∴m+n>0.
(2)证明:当x>0时,f(x)=|log2(x+1)|=log2(x+1)在(0,+∞)上为增函数.
由(1)知m2-(m+n)=m2+mn=m(m+n),且m<0,m+n>0,∴m(m+n)<0.
∴m2-(m+n)<0,0<m2<m+n.
∴f(m2)<f(m+n).
同理,(m+n)-n2=-mn-n2=-n(m+n)<0,
∴0<m+n<n2.∴f(m+n)<f(n2).
∴f(m2)<f(m+n)<f(n2).
[例2] 求证:对任意x、y∈R,都有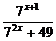 ≤5-3y+
≤5-3y+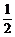 y2,并说明等号何时成立.
y2,并说明等号何时成立.
证明:72x+49≥2·7x·7=2·7x+1,
∴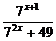 ≤
≤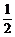 .
.
又∵5-3y+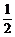 y2=
y2=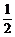 (y-3)2+
(y-3)2+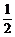 ≥
≥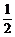 ,∴
,∴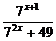 ≤5-3y+
≤5-3y+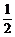 y2.
y2.
当且仅当x=1,y=3时取等号.
2.应用不等式解决应用问题时,应先弄清题意,根据题意列出不等式或函数式,再利用不等式的知识求解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com