5.了解正态分布的意义及主要性质.

4.会用样本频率分布估计总体分布.

3.会用随机抽样、系统抽样、分层抽样等常用的抽样方法从总体中抽取样本.

2.了解离散型随机变量的期望值、方差的意义，会根据离散型随机变量的分布列求出期望值、方差.

1.了解离散型随机变量的意义，会求出某些简单的离散型随机变量的分布列.

6.条形图是用其高度表示取各值的频率；直方图是用图形面积的大小表示在各区间内取值的频率；累积频率分布图是一条折线，利用任意两端值的累积频率之差表示样本数据在这两点值之间的频率.

拓展题例

[例1] (2004年辽宁省重点高中模拟题)用系统抽样法要从160名学生中抽取容量为20的样本，将160名学生随机地从1-160编号，按编号顺序平均分成20组(1-8号，9-16号，…，153-160号)，若第16组抽出的号码为126，则第1组中用抽签的方法确定的号码是___________.

解析：不妨设在第1组中随机抽到的号码为x，则在第16组中应抽出的号码为120+x.

设第1组抽出的号码为x，则第16组应抽出的号码是8×15+x=126，∴x=6.

答案：6

[例2] (2004年苏、锡、常、镇四市模拟题)某单位有职工160名，其中业务人员120名，管理人员16名，后勤人员24名.为了解职工的某种情况，要从中抽取一个容量为20的样本.若用分层抽样的方法，抽取的业务人员、管理人员、后勤人员的人数应分别为____________.

解析：分层抽样应按各层所占的比例从总体中抽取.

∵120∶16∶24=15∶2∶3，又共抽出20人，

∴各层抽取人数分别为20×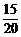=15人，20×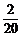=2人，20×=3人.

答案：15人、2人、3人

5.解决总体分布估计问题的一般程序如下：(1)先确定分组的组数(最大数据与最小数据之差除以组距得组数)；(2)分别计算各组的频数及频率(频率=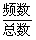)；(3)画出频率分布直方图，并作出相应的估计.

4.分层抽样的步骤：(1)分层；(2)按比例确定每层抽取个体的个数；(3)各层抽样(方法可以不同)；(4)汇合成样本.

3.系统抽样的步骤：(1)将总体中的个体随机编号；(2)将编号分段；(3)在第1段中用简单随机抽样确定起始的个体编号；(4)按照事先研究的规则抽取样本.

2.总体分布反映了总体在各个范围内取值的概率.当总体中所取不同数值比较少时，常用条形图表示相应样本的频率分布；否则，常用频率分布直方图表示相应样本的频率分布.