
5.已知正数x、y满足x+2y=1,求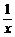 +
+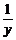 的最小值.
的最小值.
解:∵x、y为正数,且x+2y=1,
∴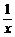 +
+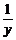 =(x+2y)(
=(x+2y)(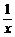 +
+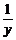 )
)
=3+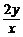 +
+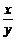 ≥3+2
≥3+2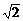 ,
,
当且仅当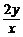 =
=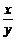 ,即当x=
,即当x=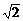 -1,y=1-
-1,y=1-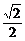 时等号成立.
时等号成立.
∴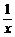 +
+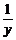 的最小值为3+2
的最小值为3+2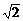 .
.
4.若a>0,b>0,ab≥1+a+b,则a+b的最小值为____________.
解析:1+a+b≤ab≤(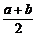 )2,
)2,
∴(a+b)2-4(a+b)-4≥0.
∴a+b≤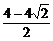 或a+b≥
或a+b≥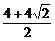 .
.
∵a>0,b>0,∴a+b≥2+2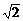 .
.
答案:2+2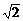
3.b g糖水中有a g糖(b>a>0),若再添m g糖(m>0),则糖水变甜了.试根据这一事实,提炼出一个不等式____________.
解析: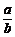 <
<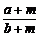 .
.
答案: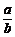 <
<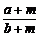
2.当x∈[-1,2]时,不等式a≥x2-2x-1恒成立,则实数a的取值范围是
A.a≥2 B.a≥1 C.a≥0 D.a≥-2
解析:当x∈[-1,2]时,x2-2x-1=(x-1)2-2∈[-2,2].
∵a≥x2-2x-1恒成立,∴a≥2.
答案:A
1.已知方程sin2x-4sinx+1-a=0有解,则实数a的取值范围是
A.[-3,6] B.[-2,6] C.[-3,2] D.[-2,2]
解析:∵a=(sinx-2)2-3,|sinx|≤1,
∴-2≤a≤6.
答案:B
5.已知不等式组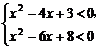 的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是____________.
的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是____________.
解析:由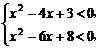 得2<x<3.
得2<x<3.
则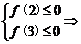 a≤9.
a≤9.
答案:(-∞,9]
●典例剖析
[例1] 函数y=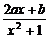 的最大值为4,最小值为-1,求常数a、b的值.
的最大值为4,最小值为-1,求常数a、b的值.
剖析:由于函数是分式函数,且定义域为R,故可用判别式法求最值.
解:由y=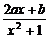 去分母整理得
去分母整理得
yx2-2ax+y-b=0. ①
对于①,有实根的条件是Δ≥0,
即(-2a)2-4y(y-b)≥0.
∴y2-by-a2≤0.又-1≤y≤4,
∴y2-by-a2=0的两根为-1和4.
∴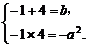 解得
解得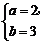 或
或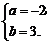
评述:这是关于函数最大值、最小值的逆向题.
深化拓展
已知x、y∈R+且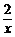 +
+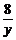 =1,求x+y的最小值.本题不难求解(读者不妨求解).
=1,求x+y的最小值.本题不难求解(读者不妨求解).
由本题的启发,你能解下列问题吗?
已知a、b是正常数,a+b=10,又x、y∈R+,
且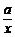 +
+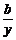 =1,x+y的最小值为18.
=1,x+y的最小值为18.
求a、b的值.
略解:x+y=(x+y)(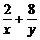 )=10+
)=10+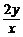 +
+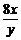 ≥10+2
≥10+2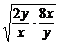 =18.
=18.
当且仅当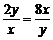 时取等号.
时取等号.
由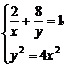 解得
解得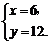
∴当x=6,y=12时,x+y的最小值为18.
同上题,x+y=(x+y)(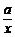 +
+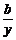 )=a+b+
)=a+b+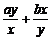 ≥a+b+2
≥a+b+2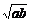 .
.
由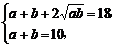 得
得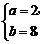 或
或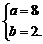
[例2] 已知a>0,求函数y=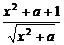 的最小值.
的最小值.
解:y=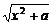 +
+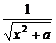 ,
,
当0<a≤1时,y=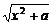 +
+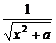 ≥2,
≥2,
当且仅当x=±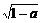 时取等号,ymin=2.
时取等号,ymin=2.
当a>1时,令t=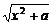 (t≥
(t≥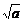 ).
).
y=f(t)=t+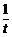 .
.
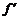 (t)=1-
(t)=1-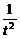 >0.
>0.
∴f(t)在[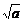 ,+∞)上为增函数.
,+∞)上为增函数.
∴y≥f(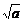 )=
)=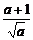 ,等号当t=
,等号当t=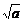 即x=0时成立,ymin=
即x=0时成立,ymin=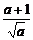 .
.
综上,0<a≤1时,ymin=2;
a>1时,ymin=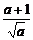 .
.
[例3] 已知函数f(x)=ax2+bx+c(a>0且bc≠0).
(1)若| f(0)|=| f(1)|=| f(-1)|=1,试求f(x)的解析式;
(2)令g(x)=2ax+b,若g(1)=0,又f(x)的图象在x轴上截得的弦的长度为l,且0<l≤2,试确定c-b的符号.
解:(1)由已知| f(1)|=| f(-1)|,有|a+b+c|=|a-b+c|,(a+b+c)2=(a-b+c)2,可得4b(a+c)=0.
∵bc≠0,∴b≠0.∴a+c=0.
又由a>0有c<0.
∵|c|=1,于是c=-1,则a=1,|b|=1.
∴f(x)=x2±x-1.
(2)g(x)=2ax+b,由g(1)=0有2a+b=0,b<0.
设方程f(x)=0的两根为x1、x2.
∴x1+x2=-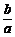 =2,x1x2=
=2,x1x2=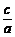 .
.
则|x1-x2|=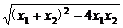 =
=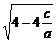 .
.
由已知0<|x1-x2|≤2,∴0≤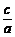 <1.
<1.
又∵a>0,bc≠0,∴c>0.∴c-b>0.
●闯关训练
夯实基础
4.已知实数x、y满足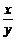 =x-y,则x的取值范围是_______.
=x-y,则x的取值范围是_______.
解析:由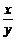 =x-y,得y2-xy+x=0.
=x-y,得y2-xy+x=0.
∵y∈R,∴Δ=x2-4x≥0.∴0≤x≤4.
∵x=0时y=0不符合题意,∴0<x≤4.
答案:0<x≤4
3.(理)如果0<a<1,0<x≤y<1,且logaxlogay=1,那么xy
A.无最大值也无最小值
B.有最大值无最小值
C.无最大值有最小值
D.有最大值也有最小值
解析:∵logax+logay≥2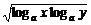 =2,
=2,
∴logaxy≥2.
∴0<xy≤a2.
答案:B
(文)已知a>b>c>0,若P=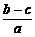 ,Q=
,Q=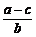 ,则
,则
A.P≥Q B.P≤Q C.P>Q D.P<Q
解析:特殊值检验.a=3,b=2,c=1.
P=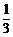 ,Q=1,P<Q.
,Q=1,P<Q.
答案:D
2.把长为12 cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是
A.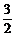
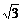 cm2 B.4 cm 2
cm2 B.4 cm 2
C.3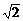 cm2 D.2
cm2 D.2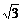 cm2
cm2
解析:设两段长分别为x cm,(12-x) cm,
则S=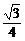 (
(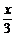 )2+
)2+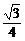 (
(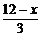 )2=
)2=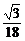 (x2-12x+72)=
(x2-12x+72)=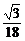 [(x-6)2+36]≥2
[(x-6)2+36]≥2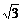 .
.
答案:D
1.已知函数f(x)=log (x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是
(x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是
A.(-∞,4] B.(-4,4]
C.(0,12) D.(0,4]
解析:∵f(x)=log (x2-ax+3a)在[2,+∞)上是减函数,
(x2-ax+3a)在[2,+∞)上是减函数,
∴u=x2-ax+3a在[2,+∞)上为增函数,且在[2,+∞)上恒大于0.
∴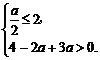
∴-4<a≤4.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com