
[方法二](空间向量)⑴ =
= =
= (
( +
+ )=
)= (
( +
+ )=
)=
[方法一]原来思路⑴取PD的中点F,FE AB,ABEF是平行四边形,BE∥AF,BE、AF分别在平面PAD外、内,故:BE∥平面PAD
AB,ABEF是平行四边形,BE∥AF,BE、AF分别在平面PAD外、内,故:BE∥平面PAD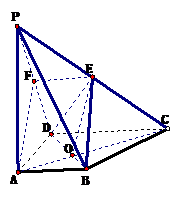
⑵如果平面EBD⊥平面ABCD,交线为BD,则过E作EO⊥BD,EO⊥平面ABCD,∵PA⊥平面ABCD∴EO∥PA ∵E为PC中点∴O为AC的中点 ∵ABCD是直角梯形∴O不在BD上,与O在BD上矛盾,平面EBD不垂直平面ABCD
例3、四棱锥P-ABCD底面是一直角梯形,AB∥CD,AB⊥AD,CD=2AB,PA⊥平面ABCD,E为PC的中点(1)求证:BE∥平面PAD;(2)平面EBD是否垂直平面ABCD,证明你的结论
设平面ADE的一个法向量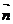 =(x,y,z),则
=(x,y,z),则 ,解得x=0,z=-2y,
,解得x=0,z=-2y, 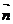 =(0,y,-2y)
=(0,y,-2y)  ∥
∥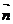 ,所以
,所以 平面
平面
故D
[另法](找平面ADE的一个法向量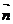 ,看
,看 是否平行于
是否平行于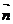 即可)
即可)

 所以
所以 平面
平面
故D
因为 所以
所以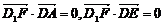
 ,
,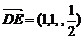
 例2、在正方体
例2、在正方体 中,E,F分别是BB1,,CD中点,问过D
中,E,F分别是BB1,,CD中点,问过D
分析:只要验证D1F是否垂直平面ADE即可
证明:设正方体棱长为1,建立如图所示坐标系D-xyz
故AE= AE时,
AE时, 平面
平面
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com