[答案]1、等边三角形；2、4|a|是其一个周期；3、①③④②；②③④①

3、α、β是两个不同的平面，m、n是平面α、β之外的两条不同直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断为条件，余下一个论断为结论，写出你认为正确的一个命题

2、函数f(x)满足对任意非零实数a及任意x有f(x+a)=,判断f(x)是否为周期函数，如果是求出它的一个周期

1、在三角形ABC中，三个内角A、B、C对应边分别为a,b,c，且A、B、C成等差数列，a、b、c成等比数列，判断三角形ABC的形状，并证明

(EF=,)

说明：（1）数学发现过程是一个探索创造的过程.是一个不断地提出猜想验证猜想的过程，合情推理和论证推理相辅相成，相互为用，共同推动着发现活动的进程。

（2）合情推理是富于创造性的或然推理，在数学发现活动中，它为演绎推理确定了目标和方向，具有提出猜想、发现结论，提供思路的作用。

（3）演绎推理是形式化程度较高的必然推理，在数学发现活动中，它具有类似于“实验”的功能，它不仅为合情推理提供了前提，而且可以对猜想作出“判决”和证明，从而为调控探索活动提供依据。

[补充习题]

练习：直线P₁P₂上有点P，若=λ，称P分的比为λ，则有，类比此结论，对于一个梯形ABCD（上底、下底分别为DC、AB），EF分梯形的高的自上而下的比为λ，求EF（用两底AB、CD表示），并证明;

再次类比，空间一个台体，上下底面面积分别为S₁、S₂，一个平行于底面的截面分高自上而下的比为λ，截面面积S与S₁、S₂满足关系______

例2、台体体积公式的推导（见教材P74―P76）

练习1：求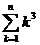

练习2：f(x)=x+e^x对一切实数a,b，a+b≤0，说明f(a)+f(b)与f(-a)+f(-b)的大小关系，并证明思考：练习2中，f(x)解析式是否必要？修改成什么条件也可以比较大小？

说明：一般的一个数学发现的过程是：计算猜想证明的思路

提出问题（n）＝＝？（见教材说明）