《空间向量与立体几何》
一、填空题
试题详情
试题详情
所成的角的大小为 ★ .
.
试题详情
3.【江苏?苏北四市】10.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
试题详情
①若 ;
;
试题详情
②若m、l是异面直线, ;
;
试题详情
③若 ;
;
试题详情
④若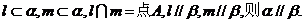
其中为真命题的是▲ ①②④ .
试题详情
试题详情
5.【江苏?苏州】已知 是两条不同的直线,
是两条不同的直线, 为两个不同的平面,
为两个不同的平面,
有下列四个命题:
试题详情
①若 ,m⊥n,则
,m⊥n,则 ;
;
试题详情
②若 ,则
,则 ;
;
试题详情
③若 ,则
,则 ;
;
试题详情
④若 ,则
,则 .
.
其中正确的命题是(填上所有正确命题的序号)_______①④________.
试题详情
6.【江苏?泰州实验】13.已知正四棱锥P―ABCD的高为4,侧棱长与底面所成的角为 ,则该正四棱锥的侧面积是
,则该正四棱锥的侧面积是  .
.
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
二、计算题
试题详情
 直棱柱
直棱柱 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,
试题详情
∠BAD=∠ADC=90°, .
.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与
平面ACB1都平行?证明你的结论.
试题详情
证明:(Ⅰ) 直棱柱 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,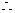 BB1⊥AC. ………………2分
BB1⊥AC. ………………2分
试题详情
又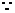 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°, ,
,
试题详情
试题详情
又 ,
, 平面BB1C1C,
平面BB1C1C,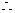 AC⊥平面BB1C1C. …7分
AC⊥平面BB1C1C. …7分
(Ⅱ)存在点P,P为A1B1的中点. ……………………………………8分
试题详情
证明:由P为A1B1的中点,有PB1‖AB,且PB1= AB.……………………9分
AB.……………………9分
试题详情
又∵DC‖AB,DC= AB,
AB,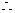 DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.…………………………11分
试题详情
又CB1 面ACB1,DP
面ACB1,DP  面ACB1,
面ACB1,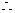 DP‖面ACB1.………………………………13分
DP‖面ACB1.………………………………13分
同理,DP‖面BCB1.…………………………………………………14分
评讲建议:
本题主要考查线面平行、垂直的的判定和证明等相关知识,第一小题要引导学生挖掘直角梯形ABCD中BC⊥AC,第二小题,要求学生熟练掌握一个常用结论:若一直线与两相交平面相交,则这条直线一定与这两平面的交线平行;同时注意问题的逻辑要求和答题的规范性,这里只需要指出结论并验证其充分性即可,当然亦可以先探求结论,再证明之,这事实上证明了结论是充分且必要的.
试题详情
2.【江苏?淮、徐、宿、连】16.(本小题满分14分)
如图,四边形ABCD为矩形,BC上平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
试题详情
 (2)设点M为线段AB的中点,点N为线段CE的中点.
(2)设点M为线段AB的中点,点N为线段CE的中点.
试题详情
求证:MN∥平面DAE.

试题详情
【解】(1)证明:因为 ,
, ,
,
试题详情
所以 ,………………………………………………2分
,………………………………………………2分
试题详情
又 ,
, ,
,
试题详情
 所以
所以 , ……………………………………………4分
, ……………………………………………4分
试题详情
又 ,所以
,所以 ……………………………………………6分
……………………………………………6分
试题详情
又 ,所以
,所以 . ……………………………………………8分
. ……………………………………………8分
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B1C1D1中,F是BC的中点,点E在D1C1上,且D1E=
【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B1C1D1中,F是BC的中点,点E在D1C1上,且D1E= D1C1,试求直线EF与平面D1AC所成角的正弦值.
D1C1,试求直线EF与平面D1AC所成角的正弦值.
试题详情
试题详情
试题详情
 为平面
为平面 的法向量,
的法向量,
试题详情
 .……8分
.……8分
试题详情
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .………………………………10分
.………………………………10分
试题详情
4.【江苏?南通】15.(本小题14分)
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
试题详情
 (1)求证:AD⊥平面BC C1 B1;
(1)求证:AD⊥平面BC C1 B1;
试题详情
(2)设E是B1C1上的一点,当 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
试题详情
解: (1)在正三棱柱中,C C1⊥平面ABC,AD 平面ABC,
平面ABC,
∴ AD⊥C C1.………………………2分
又AD⊥C1D,C C1交C1D于C1,且C C1和C1D都在面BC C1 B1内,
∴ AD⊥面BC C1 B1. ……………………………………………5分
(2)由(1),得AD⊥BC.在正三角形ABC中,D是BC的中点.…………7分
试题详情
当 ,即E为B1C1的中点时,A1E∥平面ADC1.…………………8分
,即E为B1C1的中点时,A1E∥平面ADC1.…………………8分
事实上,正三棱柱ABC-A1B1C1中,四边形BC C1 B1是矩形,且D、E分别是BC、B1C1的中点,所以B1B∥DE,B1B= DE. ……………………10分
又B1B∥AA1,且B1B=AA1,
∴DE∥AA1,且DE=AA1.
…………………………………………12分
所以四边形ADE A1为平行四边形,所以E A1∥AD.
试题详情
而E A1 面AD C1内,故A1E∥平面AD C1. …………………………14分
面AD C1内,故A1E∥平面AD C1. …………………………14分
试题详情
5.【江苏?启东中学模拟】
|
试题详情
∠ACB=900,AC=1,C点到AB1的距离为CE= ,D为AB的中点. ,D为AB的中点. (1)求证:AB1⊥平面CED; (2)求异面直线AB1与CD之间的距离; 【解】(1)∵D是AB中点,△ABC为等腰直角三角形,∠ABC=900,∴CD⊥AB又AA1⊥平面ABC,∴CD⊥AA1. ∴CD⊥平面A1B1BA ∴CD⊥AB1,又CE⊥AB1, ∴AB1⊥平面CDE; (2)由CD⊥平面A1B1BA ∴CD⊥DE ∵AB1⊥平面CDE ∴DE⊥AB1 ∴DE是异面直线AB1与CD的公垂线段 试题详情
∵CE= ,AC=1 , ∴CD= ,AC=1 , ∴CD=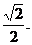 试题详情
∴ ; ; 试题详情
6.【江苏?启东中学】16.(本题满分14分,第1问4分,第2问5分,第3问5分) 如下的三个图中,分别是一个长方体截去一个角所得多面体的直观图以及它的主视图和左视图(单位:cm) (1)按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积; 试题详情
试题详情
 
【解】(1)如图 试题详情
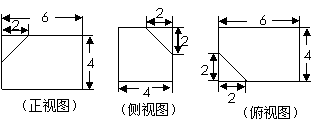  ------------4分 ------------4分
试题详情
试题详情
(3)证明:在长方体 中, 中, 试题详情
连结 ,则 ,则 . . 试题详情
试题详情
试题详情
7.【江苏?苏北四市】 16. (本题满分14分) 16. (本题满分14分) 试题详情
试题详情
求证:(1) 平面CDE; 平面CDE; 试题详情
(2)平面 平面 平面 . . 试题详情
(3)若G为 的重心,试在线段AE上确定一点F,使得GF 的重心,试在线段AE上确定一点F,使得GF 平面CDE. 平面CDE. 试题详情
【解】证明:(1) 同理, 同理,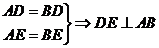 试题详情
试题详情
(2)由(1)有 平面 平面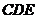 试题详情
试题详情
(3)连接AG并延长交CD于H,连接EH,则 , , 试题详情
在AE上取点F使得 ,则 ,则 ,易知GF ,易知GF 平面CDE.…………………14分 平面CDE.…………………14分 试题详情
试题详情
(I)求证: 平面 平面 ; ; 试题详情
(II)求 到平面 到平面 的距离; 的距离; 试题详情
(III)求二面角 余弦值的大小。 余弦值的大小。 试题详情
试题详情
试题详情
以 为 为 轴建立空间坐标系, 轴建立空间坐标系, 试题详情
试题详情
 , , , ,
试题详情
 , , , ,
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
故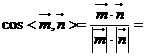  ,根据法向量的方向, ,根据法向量的方向, 试题详情
可知二面角 的余弦值大小为 的余弦值大小为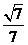 试题详情
试题详情
 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V; (Ⅱ)若F为PC的中点,求证PC⊥平面AEF; (Ⅲ)求证CE∥平面PAB. 【解】(Ⅰ)在Rt△ABC中,AB=1, 试题详情
∠BAC=60°,∴BC= ,AC=2. ,AC=2. 在Rt△ACD中,AC=2,∠CAD=60°, 试题详情
∴CD=2 ,AD=4. ,AD=4. 试题详情
∴SABCD=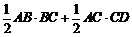 试题详情
 .……………… 3分 .……………… 3分
试题详情
则V= . ……………… 5分 . ……………… 5分 试题详情
 (Ⅱ)∵PA=CA,F为PC的中点, (Ⅱ)∵PA=CA,F为PC的中点,
∴AF⊥PC.
……………… 7分 ∵PA⊥平面ABCD,∴PA⊥CD. ∵AC⊥CD,PA∩AC=A, ∴CD⊥平面PAC.∴CD⊥PC. ∵E为PD中点,F为PC中点, ∴EF∥CD.则EF⊥PC. ……… 9分 ∵AF∩EF=F,∴PC⊥平面AEF.…… 10分 (Ⅲ)证法一: 取AD中点M,连EM,CM.则EM∥PA. 试题详情
∵EM  平面PAB,PA 平面PAB,PA 平面PAB, 平面PAB, ∴EM∥平面PAB. ……… 12分 在Rt△ACD中,∠CAD=60°,AC=AM=2, ∴∠ACM=60°.而∠BAC=60°,∴MC∥AB. 试题详情
 ∵MC ∵MC  平面PAB,AB 平面PAB,AB 平面PAB, 平面PAB,
∴MC∥平面PAB. ……… 14分 ∵EM∩MC=M, ∴平面EMC∥平面PAB. 试题详情
∵EC 平面EMC, 平面EMC, ∴EC∥平面PAB. ……… 15分 证法二: 延长DC、AB,设它们交于点N,连PN. ∵∠NAC=∠DAC=60°,AC⊥CD, ∴C为ND的中点.
……12分 ∵E为PD中点,∴EC∥PN.……14分 试题详情
∵EC  平面PAB,PN 平面PAB,PN  平面PAB, 平面PAB, ∴EC∥平面PAB. ……… 15分 试题详情
试题详情
试题详情
试题详情
(Ⅱ)证明: . . 试题详情
试题详情
试题详情
试题详情
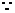  , ,
试题详情
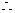  , ,
试题详情
又面 面 面 , , 试题详情
试题详情
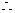  .………………….10分 .………………….10分
试题详情
 , ,
试题详情
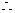  , ,
试题详情
 ,即 ,即 , ,
试题详情
 面 面 , ,
试题详情
 .………………….14分 .………………….14分
试题详情
试题详情
试题详情
(2)求二面角 的大小; 的大小; 【解】解法一: 试题详情
试题详情
则 . . 试题详情
因为 是 是 的中点, 的中点, 试题详情
所以 . . 试题详情
则 是平行四边形,因此有 是平行四边形,因此有 . . 试题详情
试题详情
则 面 面 .……………….5分 .……………….5分 试题详情
试题详情
试题详情
试题详情
又因为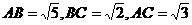  . . 试题详情
试题详情
试题详情
即:所求二面角的大小为 .……………….10分 .……………….10分 解法二: 试题详情
(1)如图,以 为原点建立空间直角坐标系, 为原点建立空间直角坐标系, 试题详情
试题详情
 . .
试题详情
易知, 是平面 是平面 的一个法向量. 的一个法向量. 试题详情
试题详情
所以 平面 平面 .……………….5分 .……………….5分 试题详情
(2) , , 试题详情
设 是平面 是平面 的一个法向量,则 的一个法向量,则 试题详情
则 得: 得: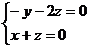 试题详情
取 . . 试题详情
显然, 为平面 为平面 的一个法向量. 的一个法向量. 试题详情
 则 则 ,结合图形可知所求二面角为锐角. ,结合图形可知所求二面角为锐角.
试题详情
所以二面角 的大小是 的大小是 .……………….10分 .……………….10分 试题详情
试题详情
(1)求证: //平面 //平面 ; ; 试题详情
(2)求证: ; ; 试题详情
(3)求三棱锥 的体积. 的体积. 试题详情
试题详情
 
(2) 试题详情
试题详情
试题详情
试题详情
(3)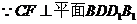 试题详情
 且 且 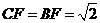
试题详情
 , ,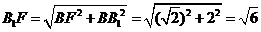
试题详情
试题详情
∴ 即 即 试题详情
 = =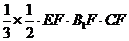
试题详情
= 试题详情
试题详情
试题详情
(Ⅰ)若 ,试指出点 ,试指出点 的位置; 的位置; 试题详情
(Ⅱ)求证: . .
试题详情
试题详情
所以 ………………………………………………………(4分) ………………………………………………………(4分) 试题详情
试题详情
试题详情
试题详情
所以 ,则 ,则 ………………………………………(10分) ………………………………………(10分) 试题详情
试题详情
而 ,所以 ,所以 ………………………(14分) ………………………(14分) 试题详情
试题详情
14.【江苏?盐城】22.(本小题满分10分) 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°. (Ⅰ)求点A到平面PBD的距离; (Ⅱ)求二面角A―PB―D的余弦值. 试题详情
【解】 解:以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则 , , …(2分) …(2分) 试题详情
(Ⅰ)设平面PDB的法向量为 , ,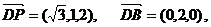 试题详情
由 , , 试题详情
试题详情
所以 = = ………………………………(5分) ………………………………(5分) 试题详情
(Ⅱ)设平面ABP的法向量 , , , , 试题详情
 , , , , 试题详情
 ,而所求的二面角与 ,而所求的二面角与 互补, 互补, 试题详情
所以二面角A―PB―D的余弦值为 ………………………………………(10分) ………………………………………(10分) 试题详情
15.【江苏?常州】16.(14分)如图,在组合体中, 是一个长方体, 是一个长方体, 是一个四棱锥, 是一个四棱锥, 试题详情
试题详情
(1) 证明: 平面 平面 ; ; 试题详情
(2) 证明: 平面 平面 。 。 【解】(略) 试题详情
| |

 中,
中, ,则
,则 与平面
与平面
 .
. ;
; ;
; ;
;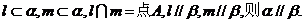
 是两条不同的直线,
是两条不同的直线, 为两个不同的平面,
为两个不同的平面, ,m⊥n,则
,m⊥n,则 ;
; ,则
,则 ;
; ,则
,则 ;
; ,则
,则 .
. ,则该正四棱锥的侧面积是
,则该正四棱锥的侧面积是  .
. 、
、 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,给出下列四个命题:
是一条直线,给出下列四个命题: ,则
,则 ;
②若
;
②若 ,则
,则 ;
; 上有两个点到
上有两个点到 的距离相等,则
的距离相等,则 ; ④若
; ④若 ,则
,则 。
。 高为2,侧棱与底面成
高为2,侧棱与底面成 角,则点A到侧面
角,则点A到侧面 的距离是
的距离是 
 9.【江苏?盐城】13.如图,在三棱锥
9.【江苏?盐城】13.如图,在三棱锥 中,
中,  、
、 、
、 两两垂直,且
两两垂直,且 .设
.设 是底面
是底面 内一点,定义
内一点,定义 ,其中
,其中 、
、 、
、 分别是三棱锥
分别是三棱锥 、 三棱锥
、 三棱锥 、三棱锥
、三棱锥 的体积.若
的体积.若 ,且
,且 恒成立,则正实数
恒成立,则正实数 的最小值为____▲1____.
的最小值为____▲1____. 直棱柱
直棱柱 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形, .
. 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,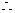 BB1⊥AC. ………………2分
BB1⊥AC. ………………2分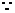 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°, ,
, ,∠CAB=45°,∴
,∠CAB=45°,∴ ,
,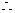 BC⊥AC.………………5分
BC⊥AC.………………5分 ,
, 平面BB
平面BB AC⊥平面BB
AC⊥平面BB AB.……………………9分
AB.……………………9分 AB,
AB, DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1, 面ACB1,DP
面ACB1,DP  面ACB1,
面ACB1, DP‖面ACB1.………………………………13分
DP‖面ACB1.………………………………13分 (2)设点M为线段AB的中点,点N为线段CE的中点.
(2)设点M为线段AB的中点,点N为线段CE的中点.

 ,
, ,
, ,………………………………………………2分
,………………………………………………2分 ,
, ,
, 所以
所以 , ……………………………………………4分
, ……………………………………………4分 ,所以
,所以 ……………………………………………6分
……………………………………………6分 ,所以
,所以 . ……………………………………………8分
. ……………………………………………8分 的中点
的中点 ,连接
,连接 ,因为点
,因为点 为线段
为线段 的中点.
的中点. ||
|| ,且
,且 , ……………………………………………………10分
, ……………………………………………………10分 是矩形,点
是矩形,点 为线段
为线段 的中点,所以
的中点,所以 ||
|| ,且
,且 ,
, ||
|| ,且
,且 ,故四边形
,故四边形 是平行四边形,所以
是平行四边形,所以 ||
|| …………12分
…………12分 平面
平面 ,
, 平面
平面 ,所以
,所以 ∥平面
∥平面 . …………………14分
. …………………14分 【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B
【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B D
D 为单位正交基底,建立如图所示坐标系
为单位正交基底,建立如图所示坐标系 ,则各点的坐标分别为
,则各点的坐标分别为 ,
, ,
,
 ,……………………2分
,……………………2分 所以
所以 ,
, , ……………………4分
, ……………………4分 为平面
为平面 的法向量,
的法向量, .……8分
.……8分 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .………………………………10分
.………………………………10分 (1)求证:AD⊥平面BC C1 B1;
(1)求证:AD⊥平面BC C1 B1; 的值为多少时,
的值为多少时, 平面ABC,
平面ABC, ,即E为B
,即E为B 面AD C1内,故A1E∥平面AD C1. …………………………14分
面AD C1内,故A1E∥平面AD C1. …………………………14分