练习册

  • 练习册
  • 试题

    题目列表(包括答案和解析)

     0  100069  100077  100083  100087  100093  100095  100099  100105  100107  100113  100119  100123  100125  100129  100135  100137  100143  100147  100149  100153  100155  100159  100161  100163  100164  100165  100167  100168  100169  100171  100173  100177  100179  100183  100185  100189  100195  100197  100203  100207  100209  100213  100219  100225  100227  100233  100237  100239  100245  100249  100255  100263  447348 

    5．A 6．解：人数分布条形图如下

    频率分布条形图如下

    试题详情

    1．C　 2．200　 3．B　 4．B

    试题详情

    7．下表给出了某学校120名12岁男生的身高统计分组与频数(单位：cm)．

    区间
    		 [122,126)
    		 [126,130)
    		 [130,134)
    		 [134,138)
    		 [138,142)
    		 [142,146)
    		 [146,150)
    		 [150,154)
    		 [154,158)
    人数
    		 5
    		 8
    		 10
    		 22
    		 33
    		 20
    		 11
    		 6
    		 5

    (1)列出样本的频率分布表(含累积频率)；

    (2)画出频率分布直方图；

    (3)根据累积频率分布，估计小于134的数据约占多少百分比．

    [解答]

    试题详情

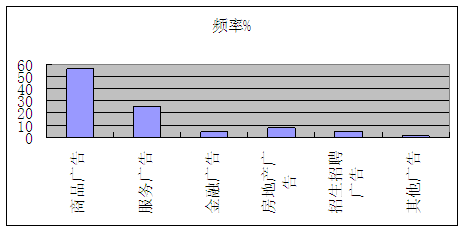
    6．用条形图表示下表中关注不同广告的人数、频率。

    广告类型
    		 人数
    		 比例
    		 频率%
    商品广告
    		 112
    		 0.560
    		 56
    服务广告
    		 51
    		 0.255
    		 25.5
    金融广告
    		 9
    		 0.045
    		 4.5
    房地产广告
    		 16
    		 0.080
    		 8
    招生招聘广告
    		 10
    		 0.050
    		 5
    其他广告
    		 2
    		 0.010
    		 1
    合计
    		 200
    		 1.000
    		 100

    [拓展尝新]

    试题详情

    5.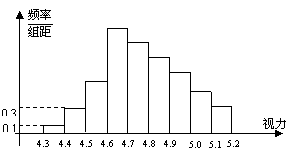(江西卷)为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为(　 )

    　　　 A．0,27,78　　　　　　　 B．0,27,83

    　　　 C．2.7,78　　　　　　　　 D．2.7,83

    试题详情

    3. 一个容量为32的样本，已知某组的样本的频率为0.25，则该组样本的频数为(　 )

    A．2　　　 B．4　　　　 C．6　　　 D．8

    试题详情

    2. 一个容量为n的样本，分成若干组，已知某数的频数和频率分别为50和0.25，则n＝　　　．

    试题详情

    1.在用样本频率估计总体分布的过程中，下列说法中正确的是( )

    A．总体容量越大，估计越精确　　　　　　　　　　　 B．总体容量越小，估计越精确C．样本容量越大，估计越精确　　　　　　　　　　 　D．样本容量越小，估计越精确

    试题详情

    2．经典回放：

    例1 ：为检测某产品的质量，抽取了一个容量为30的样本，检测结果为一级品5件，二级品8件，三级品13件，次品4件。

    ⑴ 列出样本的频率分布表；

    ⑵此种产品为二级品或三级品的概率？

    ⑶能否画出样本分布的条形图？

    分析：当总体中的个体取不同数值很少时，可用频率分布表或频率分布条形图估计总体分布。解：频率分布表如下：

    产品
    		 频数
    		 频率
    一级品
    		 5
    		 0.17
    二级品
    		 8
    		 0.27
    三级品
    		 13
    		 0.43
    次品
    		 4
    		 0.13
    合计
    		 30
    		 1

    频率分布条形图：

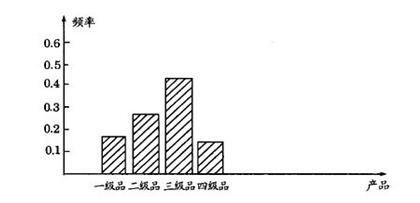
    点评：频率分布表中通常有频数、累计频数，频率、累计频率等。其中所有频数的和即样本容量的大小，而所有频率的和恰好为1。

    例2：为了了解某地区高三学生的身体发育情况，抽查了地区内100名年龄为17.5岁~18岁的男生的体重情况,结果如下(单位:kg)

    56.5
    		 69.5
    		 65
    		 61.5
    		 64.5
    		 66.5
    		 64
    		 64.5
    		 76
    		 58.5
    72
    		 73.5
    		 56
    		 67
    		 70
    		 57.5
    		 65.5
    		 68
    		 71
    		 75
    62
    		 68.5
    		 62.5
    		 66
    		 59.5
    		 63.5
    		 64.5
    		 67.5
    		 73
    		 68
    55
    		 72
    		 66.5
    		 74
    		 63
    		 60
    		 55.5
    		 70
    		 64.5
    		 58
    64
    		 70.5
    		 57
    		 62.5
    		 65
    		 69
    		 71.5
    		 73
    		 62
    		 58
    76
    		 71
    		 66
    		 63.5
    		 56
    		 59.5
    		 63.5
    		 65
    		 70
    		 74.5
    68.5
    		 64
    		 55.5
    		 72.5
    		 66.5
    		 68
    		 76
    		 57.5
    		 60
    		 71.5
    57
    		 69.5
    		 74
    		 64.5
    		 59
    		 61.5
    		 67
    		 68
    		 63.5
    		 58
    59
    		 65.5
    		 62.5
    		 69.5
    		 72
    		 64.5
    		 75.5
    		 68.5
    		 64
    		 62
    65.5
    		 58.5
    		 67.5
    		 70.5
    		 65
    		 66
    		 66.5
    		 70
    		 63
    		 59.5

    试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计

    解:按照下列步骤获得样本的频率分布.

    (1)求最大值与最小值的差.在上述数据中，最大值是76，最小值是55，它们的差(又称为极差)是76-55=21)所得的差告诉我们，这组数据的变动范围有多大.

    (2)确定组距与组数.如果将组距定为2，那么由21÷2=10.5，组数为11，这个组数适合的.于是组距为2，组数为11.

    (3)决定分点.根据本例中数据的特点，第1小组的起点可取为54.5，第1小组的终点可取为56.5，为了避免一个数据既是起点，又是终点从而造成重复计算，我们规定分组的区间是“左闭右开”的.这样，所得到的分组是

    ［54.5，56.5)，［56.5，58.5)，…，［74.5，76.5).

    　 (4)列频率分布表,如表①　　　　 频率分布表

    分组
    		 频数累计
    		 频数
    		 频率
    ［54.5，56.5)
    		 2
    		 2
    		 0.02
    ［56.5，58.5)
    		 8
    		 6
    		 0.06
    ［58.5，60.5)
    		 18
    		 10
    		 0.10
    ［60.5，62.5)
    		 28
    		 10
    		 0.10
    ［62.5，64.5)
    		 42
    		 14
    		 0.14
    ［64.5，66.5)
    		 58
    		 16
    		 0.16
    ［66.5，68.5)
    		 71
    		 13
    		 0.13
    ［68.5，70.5)
    		 82
    		 11
    		 0.11
    ［70.5，72.5)
    		 90
    		 8
    		 0.08
    ［72.5，74.5)
    		 97
    		 7
    		 0.07
    ［74.5，76.5)
    		 100
    		 3
    		 0.03
    合计
    		 　
    		 100
    		 1.00

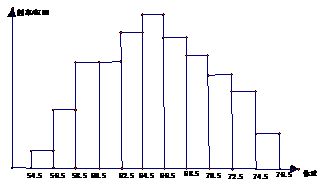    (5)绘制频率分布直方图.频率分布直方图如图所示

    在得到了样本的频率后，就可以对相应的总体情况作出估计.例如可以估计体重在［64.5，66.5)kg的学生最多，约占学生总数的16%；体重小于58.5kg的学生较少，约占8%；等等

    点评：由于图中各小长方形的面积等于相应各组的频率，这个图形的面积反映了数据落在各个小组的频率的大小.在反映样本的频率分布方面，频率分步表比较准确，频率分布直方图比较直观，它们起着相互补充的作用.

    [同步训练]

    试题详情


    同步练习册答案