
题目列表(包括答案和解析)
6. (本小题满分12分)
已知函数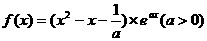 .
.
(Ⅰ)当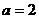 时,求
时,求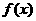 的的单调区间;
的的单调区间;
(Ⅱ)若对于任意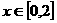 ,恒有
,恒有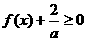 恒成立,求
恒成立,求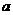 的取值范围.
的取值范围.

∴ 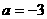 ……
5分
……
5分
(Ⅱ)由(Ⅰ)知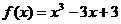 ,
, 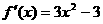 解
解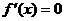 得
得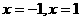
因为函数f(x)的定义域为[-1,3],故可列下表:
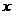 范围 范围 |
-1 |
(-1,1) |
1 |
(1,3) |
3 |
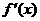 符号 符号 |
0 |
 - - |
0 |
+ |
|
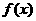 单调性 单调性 |
5 |
↘ |
极小值1 |
↗ |
21 |
所以f(x)在x=1处取得最小值1,在x=3处取得最大值21,

5.(本小题满分12分)
甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮”各一个),现以投掷一个骰子的方式进行游戏,规则如下:当向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定:掷骰子的次数达9次时,或在此前某人已赢得对方所有的福娃时游戏终止。记游戏终止时投掷骰子的次数为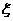 .
.
(Ⅰ)求掷骰子的次数为7的概率;
(Ⅱ)求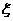 的数学期望E
的数学期望E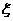 .
.
4. (本小题满分12分)
(本小题满分12分)
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,
侧棱长是,D是AC的中点.
(Ⅰ)求证:B1C//平面A1BD;
(Ⅱ)求二面角A-A1B-D的大小.
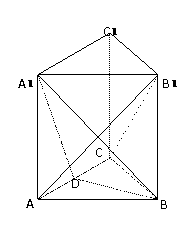
3.(本小题满分12分)
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,
∠ABC=60°,PA⊥底面ABCD,PA=AB=1.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求点A到平面PCD的距离.
 设数列
设数列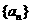 对一切
对一切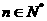 ,满足
,满足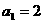 ,
,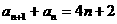 .
.
试用数学归纳法证明: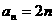 .
.
2.(本小题满分12分)
已知f(x)=x3+ax+3在x=1处取得极值.
(Ⅰ)求a的值;(Ⅱ)求函数f(x)在区间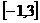 上的值域.
上的值域.
12.过点A(1,1)作拋物线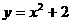 的切线,切点分别为
的切线,切点分别为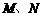 ,则
,则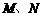 两点纵坐标之和为
两点纵坐标之和为
A.2 B.6 C.10 D.-1
11.如图,在长方体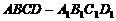 中,点E、F分别在棱A1D1、AB上滑动,P是线段EF的中点,且线段EF的长恒等于2,棱AA1的长小于2,则P、A两点间的距离为
中,点E、F分别在棱A1D1、AB上滑动,P是线段EF的中点,且线段EF的长恒等于2,棱AA1的长小于2,则P、A两点间的距离为
A.1 B.2
C.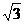 D.与长方体棱长有关
D.与长方体棱长有关
10. 如图,正方体
如图,正方体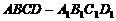 中,点O是底面ABCD的中心,点M、N分别为DD1、D1C1的中点,则直线OM
中,点O是底面ABCD的中心,点M、N分别为DD1、D1C1的中点,则直线OM
A.与AC、MN都不垂直
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC、MN都垂直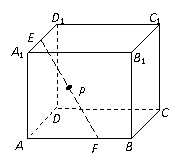
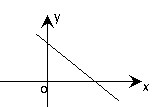
9.函数y=f(x)的图像经过原点,且它的导函数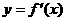 的图像是如图所示的一条直线,则
的图像是如图所示的一条直线,则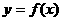 的图像一定不经过
的图像一定不经过
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8. 已知
已知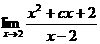 存在,则实数c的值为
存在,则实数c的值为
A.3 B.-3 C.2 D.-2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com