
题目列表(包括答案和解析)
1.解析视屏:
(1) 频率分布表:当总体很大或不便于获得时,可以用样本的频率分布来估计总体的频率分布。我们把反映总体频率分布的表格为频率分布表。
(2) 编制频率分布表的步骤:
① 求全距,决定组数和组距,组距= ;
;
② 分组,区间一般左闭右开(为了遵循统计分组穷尽和互斥原则,所以统计上规定,凡是总体某一个单位的变量值是相邻两组的界限值,这一个单位归入作为下限值的那一组内,即所谓“上限不在内”原则);
⑶ 登记频数,计算频率,列出频率分布表。
(3) 条形图:条形图是用宽度相同的条形的高度或长度来表示数据变动的图形。条形图可以横置也可以纵置,纵置时又称为柱形图,也就是说,当各类别放在纵轴时,称为条形图;当各类别放在横轴时,称为柱形图。
(4) 频率分布直方图:直方图是用矩形的宽度和高度来表示频率分布的图形(在平面直角坐标中,横轴表示数据分组,即各组组距,纵轴表示频率)。
(5)直方图与条形图的不同点:
① 条形图是用条形的长度表示各类别频数的多少,其宽度(表示类别)是固定的;直方图是用面积表示各组频率的多少,矩形的高度表示每一组的频率除以组距,宽度则表示各组的组距,因此其高度与宽度均有意义。
② 此外,由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。
2.学法指导:
当总体中的个体取不同数值很少时,可用频率分布表或频率分布条形图估计总体分布;当总体中的个体取不同数值较多,甚至无限时,可用频率分布表或频率分布直方图估计总体分布。
[教师在线]
1.学习目标:
体会分布的意义和作用,学会列频率分布表,会画频率分布条形图、直方图,会用频率分布表或分布条形图、直方图估计总体分布,并作出合理解释。在解决问题过程中,进一步体会用样本估计整体的思想,认识统计的实际作用,初步经历收集数据到统计数据的全过程,体会统计思维与确定性思维的差异。
22、(本小题满分12分) 如图,V是边长为4的菱形ABCD所在平面外一点,
并且∠BAD=120°,VA=3,VA⊥底面ABCD,O是AC,BD的交点,OE⊥VC于E.
求:(1)点V到CD的距离;
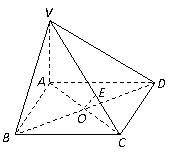 (2)异面直线VC与BD的距离;
(2)异面直线VC与BD的距离;
21. (本小题满分12分)在棱长为1的正方体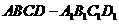 中,
中,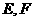 分别
分别
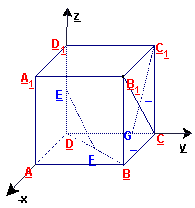 是
是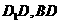 的中点,
的中点,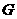 在棱
在棱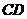 上,且
上,且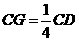 ,应用空间
,应用空间
向量方法求解下列问题.
(Ⅰ)求证: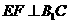 ;
;
(Ⅱ)求EF与 所成的角的余弦;
所成的角的余弦;
20. (本小题满分12分)有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱都相切,第三个球通过这个正方体的各个顶点,求这三个球的表面积之比。
19. (本小题满分12分)在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个。现从中任取出一球确定颜色后放回盒子里,再取下一个球。重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球。 求: (1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率。
18.(本小题满分12分)、如果曲线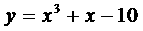 的某一切线 与直线y=4x+3平行,求切点坐标与切线方程。
的某一切线 与直线y=4x+3平行,求切点坐标与切线方程。
17.
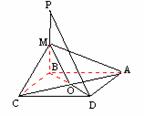 (本小题满分10分)如图,已知P为
(本小题满分10分)如图,已知P为 ABCD所在平面外一点,M为PB的中点,求证:PD∥平面MAC. (10分)
ABCD所在平面外一点,M为PB的中点,求证:PD∥平面MAC. (10分)
16、 平面内n条直线任意两条都相交,任意三条不共点,若f(n)表示n条直线交点的个数,则f(n+1)-f(n)=_____
平面内n条直线任意两条都相交,任意三条不共点,若f(n)表示n条直线交点的个数,则f(n+1)-f(n)=_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com