
题目列表(包括答案和解析)
7. 已知点P在抛物线y2 = 4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
已知点P在抛物线y2 = 4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
 A. (
A. (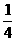 ,-1) B. (
,-1) B. (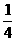 ,1) C. (1,2) D. (1,-2)
,1) C. (1,2) D. (1,-2)
6. 由直线
由直线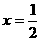 ,x=2,曲线
,x=2,曲线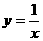 及x轴所围图形的面积是( )
及x轴所围图形的面积是( )
 A.
A. 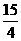 B.
B.
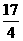 C.
C.
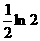 D.
D.
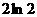
5.
 设
设 ,若函数
,若函数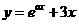 ,
, 有大于零的极值点,则( )
有大于零的极值点,则( )
 A.
A.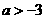 B.
B.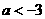 C.
C.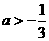 D.
D.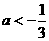
4. 已知命题
已知命题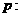 所有有理数都是实数,命题
所有有理数都是实数,命题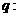 正数的对数都是负数,则下列命题中为真命题的是( )
正数的对数都是负数,则下列命题中为真命题的是( )
 A.
A.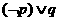 B.
B.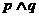 C.
C.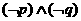 D.
D.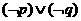
3. 若变量
若变量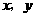 满足
满足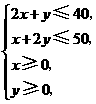 则
则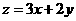 的最大值是( )
的最大值是( )
 A.90 B.80 C.70 D.40
A.90 B.80 C.70 D.40
2.某校共有学生2000名,各年级男、女生人数如表1.已知在全校 学生中随机抽取1名,
 抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
 A.24 B.18 C.16 D.12 表1
A.24 B.18 C.16 D.12 表1
1. 已知
已知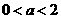 ,复数
,复数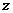 的实部为
的实部为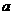 ,虚部为1,则
,虚部为1,则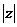 的取值范围是( )
的取值范围是( )
 A.
A.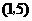 B.
B.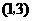 C.
C.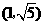 D.
D.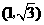
|
|
一年级 |
二年级 |
三年级 |
|
女生 |
373 |
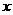 |
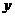 |
|
男生 |
377 |
370 |
 |
22.(本小题满分14分)
已知函数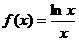 ,
,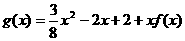 .
.
(Ⅰ)求函数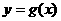 的单调区间;
的单调区间;
(Ⅱ)证明: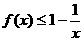 在其定义域内恒成立,并比较
在其定义域内恒成立,并比较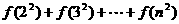 与
与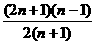 (n
(n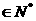 且
且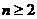 )的大小.
)的大小.
(Ⅲ)若函数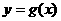 在
在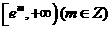 上有零点,求
上有零点,求 的最大值;
的最大值;
21.(本小题满分12分)
甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润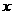 (元)与年产量
(元)与年产量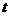 (吨)满足函数关系
(吨)满足函数关系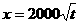 ,若乙方每生产一吨产品必须赔付甲方
,若乙方每生产一吨产品必须赔付甲方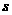 元(以下称
元(以下称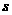 为赔付价格)
为赔付价格)
(Ⅰ)将乙方的年利润 (元)表示为年产量
(元)表示为年产量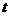 (吨)的函数,并求出乙方获得最大利润的年产量
(吨)的函数,并求出乙方获得最大利润的年产量
(Ⅱ)甲方每年受乙方生产影响的经济损失金额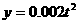 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格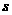 是多少?
是多少?
20.(本小题满分12分)
一台设备由三大部件构成,在设备运转中,一天之内各部件需要调整的概率分别为0.1、0.2、0.3,假设各部件的状态相互独立。(以下结果均用小数表示)
(Ⅰ)求一天之内恰有一个部件需要调整的概率;
(Ⅱ)求一天之内至少有两个部件需要调整的概率;
(Ⅲ)用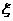 表示一天之内需要调整的部件数,求
表示一天之内需要调整的部件数,求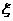 的数学期望 。
的数学期望 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com