
题目列表(包括答案和解析)
4.下列命题中是真命题的为 ( ▲ )
A. ,
,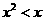 B.
B. ,
,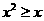
C.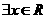 ,
,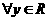 ,
,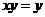 D.
D. ,
,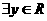 ,
,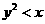
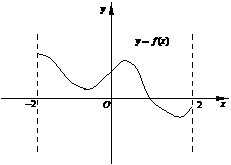
3.函数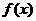 在
在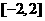 内的图象如图所示,若函数
内的图象如图所示,若函数
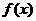 的导函数
的导函数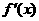 的图象也是连续不间断的,则
的图象也是连续不间断的,则
导函数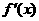 在
在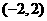 内有零点
( ▲ )
内有零点
( ▲ )
A. 个 B.
个 B.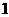 个
个
C.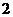 个 D.至少
个 D.至少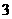 个
个
2.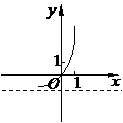
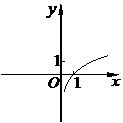
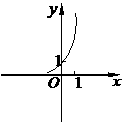
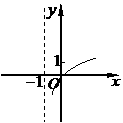 函数
函数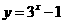 的图象大致是
( ▲ )
的图象大致是
( ▲ )
 A.
B.
C.
D.
A.
B.
C.
D.
有一项是符合题目要求的.
1.设集合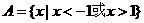 ,
,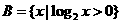 ,则
,则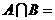 ( ▲ )
( ▲ )
A.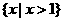 B.
B.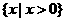
C.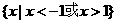 D.
D.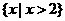
22.(本小题满分12分)已知函数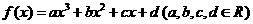 的图象与
的图象与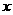 轴交于
轴交于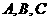 三点.若点
三点.若点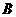 的坐标为
的坐标为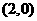 ,且函数
,且函数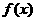 在区间
在区间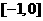 和
和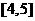 上有相同的单调性,在区间
上有相同的单调性,在区间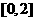 和
和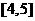 上有相反的单调性.
上有相反的单调性.
(1)求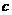 的值;
的值;
(2)求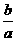 的取值范围;
的取值范围;
(3)求 的最大值和最小值.
的最大值和最小值.
慈溪市2008学年第二学期高二期末测试
21.(本小题满分10分)已知抛物线 :
: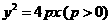 ,焦点为
,焦点为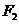 ,其准线与
,其准线与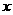 轴
轴
交于点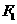 ;椭圆
;椭圆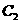 :分别以
:分别以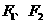 为左、右焦点,其离心率
为左、右焦点,其离心率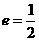 ;且抛物线
;且抛物线 和椭圆
和椭圆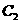 的一个交点记为
的一个交点记为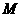 .
.
(1)当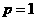 时,求椭圆
时,求椭圆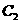 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线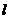 经过椭圆
经过椭圆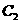 的右焦点
的右焦点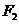 ,且与抛物线
,且与抛物线 相交于
相交于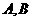
两点,若弦长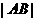 等于
等于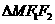 的周长,求直线
的周长,求直线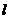 的方程.
的方程.
20.(本小题满分10分)已知定义在区间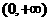 上的函数
上的函数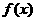 满足:对
满足:对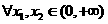
恒有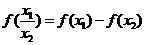 ,且当
,且当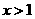 时,
时,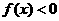 .
.
(1)求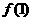 的值;
的值;
(2)证明:函数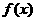 在区间
在区间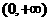 上为单调递减函数;
上为单调递减函数;
(3)若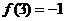 ,
,
(ⅰ)求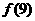 的值;
的值;
(ⅱ)解不等式: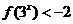 .
.
19.(本小题满分10分)用水清洗一堆蔬菜,据科学测定,其效果如下:用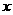 单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比为
单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比为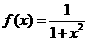 .
.
(1)因为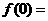 ▲ ,所以
▲ ,所以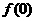 的实际意义是 ▲ (后一个▲处请选择下列之一);
的实际意义是 ▲ (后一个▲处请选择下列之一);
A.表示没有用水清洗时,蔬菜上的农药量;
B.表示没有用水清洗时,蔬菜上的农药量没有变化;
C.表示没有用水清洗.
(2)现用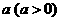 单位量的水去清洗一堆蔬菜,方案一:用
单位量的水去清洗一堆蔬菜,方案一:用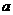 单位量的水清洗一次;
单位量的水清洗一次;
方案二:把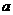 单位量的水平均分成
单位量的水平均分成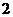 份后清洗两次.试问:哪种方案比较好(即清洗后蔬菜上残留的农药量比较少)?请说明理由.
份后清洗两次.试问:哪种方案比较好(即清洗后蔬菜上残留的农药量比较少)?请说明理由.
(为方便计算,可以假设清洗前蔬菜上的农药量为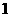 ,清洗后残留的农药量:方案一的记为
,清洗后残留的农药量:方案一的记为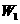 ,方案二的记为
,方案二的记为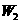 ).
).
18.(本小题满分10分)已知函数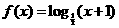 ,当点
,当点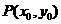 在函数
在函数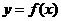 的
的
图象上移动时,点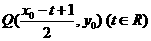 在函数
在函数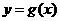 的图象上移动.
的图象上移动.
(1)若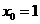 ,且点
,且点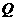 也在函数
也在函数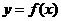 的图象上,求
的图象上,求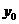 ,
,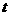 的值;
的值;
(2)当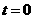 时,求函数
时,求函数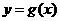 的解析式.
的解析式.
17.符号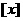 表示不超过
表示不超过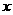 的最大整数,如
的最大整数,如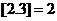 ,
,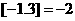 .若定义函数
.若定义函数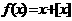 ,
,
则下列命题中所有不正确命题的序号为 ▲ .
①函数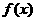 的定义域为
的定义域为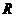 ; ②函数
; ②函数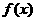 的值域为
的值域为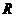 ; ③函数
; ③函数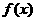 是奇函数;
是奇函数;
④函数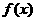 是周期函数; ⑤函数
是周期函数; ⑤函数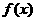 是
是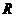 上的增函数.
上的增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com