
题目列表(包括答案和解析)
2.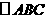 中,
中,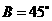 ,
,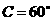 ,
,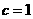 ,则最短边的边长等于
( )
,则最短边的边长等于
( )
A 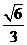 B
B 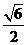 C
C 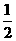 D
D 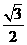
1.已知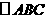 中,
中,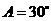 ,
,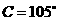 ,
,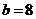 ,则等于
( )
,则等于
( )
A 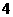 B
B 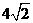 C
C 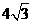 D
D 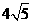
6.求解三角形应用题的一般步骤: (1)分析:分析题意,弄清已知和所求;
(2)建模:将实际问题转化为数学问题,写出已知与所求,并画出示意图; (3)求解:正确运用正、余弦定理求解;
(4)检验:检验上述所求是否符合实际意义。
5.解题中利用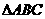 中
中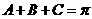 ,以及由此推得的一些基本关系式进行三角变换的运算,如:
,以及由此推得的一些基本关系式进行三角变换的运算,如: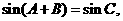
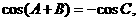
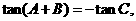
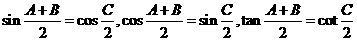 .
.
4.判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式.
2、已知两边和他们的夹角,求第三边和其他两角.
2、已知两角和其中一边的对角,求其他边角.
(2)两类余弦定理解三角形的问题:1、已知三边求三角.
3.(1)两类正弦定理解三角形的问题:1、已知两角和任意一边,求其他的两边及一角.
2.余弦定理:
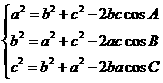 或
或 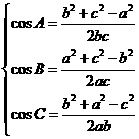 .
.
1.正弦定理: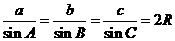 或变形:
或变形: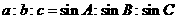 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com