
题目列表(包括答案和解析)
8、有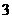 个相识的人某天各自乘同一列火车外出,假设这列火车共有
个相识的人某天各自乘同一列火车外出,假设这列火车共有 节车厢,那么至少有两人在同一车厢内相遇的概率为( )
节车厢,那么至少有两人在同一车厢内相遇的概率为( )
A、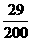 B、
B、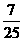 C、
C、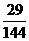 D、
D、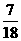
7、在等差数列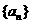 中,
中,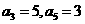 ,则
,则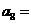 ( )
( )
A、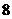 B、
B、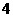 C、
C、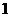 D、
D、
6、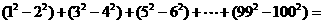
A、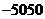 B、
B、 C、
C、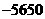 D、
D、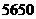
5、五种不同的商品在货架上排成一排,甲,乙两种商品必须排在一起的不同的排法有( )
A、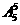 B、
B、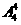 C、
C、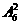 D、
D、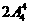
4、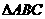 中,
中,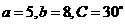 ,则
,则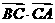 的值为( )
的值为( )
A、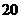 B、
B、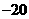 C、
C、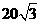 D、
D、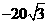
3、 设函数
设函数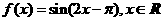 ,则
,则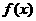 是(
)
是(
)
A、
最小正周期为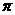 的奇函数
B、最小正周期为
的奇函数
B、最小正周期为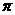 的偶函数
的偶函数
C、
最小正周期为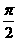 的奇函数
D、最小正周期为
的奇函数
D、最小正周期为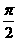 的偶函数
的偶函数
2、一个单位有 名职工,其中不到
名职工,其中不到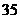 岁的人有
岁的人有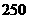 人,
人,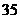 岁到
岁到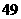 岁的人有
岁的人有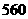 人,
人, 岁以上的人有
岁以上的人有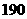 人,要从中抽取一个容量为
人,要从中抽取一个容量为 的样本,较为恰当的抽样方法是( )
的样本,较为恰当的抽样方法是( )
A、简单随机抽样 B、分层抽样 C、系统抽样 D、以上方法均可
1、设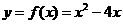 ,使
,使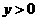 成立的一个必要非充分条件是( )
成立的一个必要非充分条件是( )
A、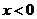 B、
B、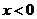 或
或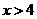 C、
C、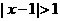 D、
D、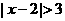
(17)(本小题满分10分)
已知△ABC的内角A、B、C所对的边分别为a,b,c,
且a=2, cosB=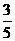 .
.
(1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值. 

(18)(本小题满分12分)
已知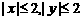 ,点P的坐标为
,点P的坐标为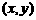 .
.
(1)求当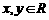 时,P满足
时,P满足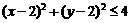 的概率;
的概率;
(2)求当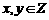 时,P满足
时,P满足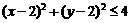 的概率.
的概率.
(19)(本小题满分12分)
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
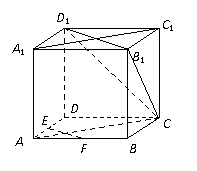 (1)求证:EF∥平面CB1D1;
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
(20)(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量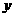 (升)关于行驶速度
(升)关于行驶速度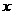 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: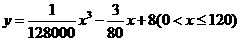 .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(21) (本小题满分12分)
已知椭圆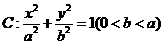 的离心率为
的离心率为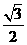 ,且经过点
,且经过点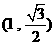
(Ⅰ)求椭圆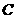 的方程;
的方程;
(Ⅱ)是否存在经过点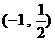 的直线
的直线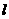 ,它与椭圆
,它与椭圆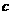 相交于
相交于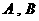 两个不同点,且满足
两个不同点,且满足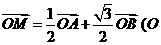 为坐标原点)关系的点
为坐标原点)关系的点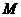 也在椭圆
也在椭圆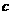 上,如果存在,求出直线
上,如果存在,求出直线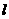 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。

(22) (本小题满分12分)
已知等比数列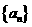 中,
中,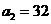 ,
,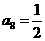 ,
,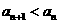 .
.
(1)求数列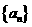 的通项公式;
的通项公式;
(2)设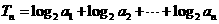 ,求
,求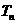 的最大值及相应的
的最大值及相应的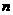 值.
值.
2008-2009学年度第二学期高二质量检测
16.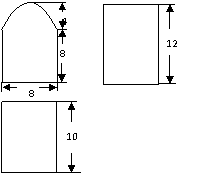 (加)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
(加)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 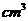 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com