
题目列表(包括答案和解析)
5、命题“若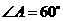 ,则
,则 是等边三角形”的否命题是( )
是等边三角形”的否命题是( )
A.假命题 B.原命题的逆否命题
C.与原命题的逆否命题同真或同假 D.与原命题的逆命题同真
4、 下列各对命题的相互关系怎样,是否等价?
(1)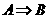 和
和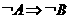 ;_____________.
(2)
;_____________.
(2)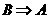 和
和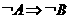 ;_____________.
(3)
;_____________.
(3)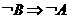 和
和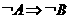 ;_____________.
;_____________.
3、将下列命题改写成“若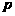 ,则
,则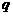 ”的形式.并写出它的逆命题、否命题和逆否命题,然后判断它们的真假:
”的形式.并写出它的逆命题、否命题和逆否命题,然后判断它们的真假:
(1)两条直线相交有且只有一个交点;
(2)线段的平分线上的点到这条线段两个端点的距离相等;
(3)矩形的对角线相等。
(4)正方形的四条边相等.
(5)若a,b都是偶数,则a+b是偶数
2、思考? 你认为哪些类型的问题宜用反证法证明?(教师引导学生给出)
答案:以下几种形式的命题常用反证法证明:
(1)某些命题的结论是否定形式,如不是、不能、不存在等; (2)某些命题的结论以至多、至少、唯一等形式出现; (3)某些命题的结论的反面非常明显或结论的反面容易证明; (4)某些命题的直接证法较困难.
1. 写出下列命题的逆命题、否命题及逆否命题,并判断它们的真假.
(1)若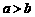 ,则
,则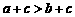 ;
;
(2)全等三角形一定是相似三角形;
(3)若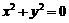 ,则
,则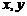 全为0;
全为0;
(4)函数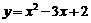 有两个零点;
有两个零点;
(5)同位角相等,两直线平行;
(6)线段垂直平分线上的点与这条线段两个端点的距离相等.
例 1 证明:若x2+y2=0 , 则x=y=0 .
写出下列命题的逆命题、否命题及逆否命题,并分别判断它们的真假.
问题1:若f(x)是正弦函数,则f(x)是周期函数.
问题2:如果x>10 , 那么x>0 .
问题3:若b2-4ac=0 , 则方程ax2+bx+c=0 (a≠0)有两个相等的实根.
问题4:已知a,b∈R , 若a=0 , 则ab=0 .
问题5:若x2-3x+2=0 ,则x=2 .
思考1? 观察上面5个例子中的原命题、逆命题、否命题以及逆否命题,你能说出每个例子中任意两个命题之间的相互关系吗?
四种命题的形式和关系如下图:(教师引导学生归纳给出)
由原命题构成道命题只要将 和 换位就可以.由原命题构成否命题只要 和 分别否定为 和 ,但 和 不必换位.由原命题构成逆否命题时不但要将 和 换位,而且要将换位后的 和 否定·
原命题为真,它的逆命题不一定为真. 原命题为真,它的否命题不一定为真. 原命题为真,它的逆否命题一定为真. 因为互为逆否命题同真同假,所以讨论四种命题的真假性只讨论原命题和逆否命题中的一个,逆命题和否命题中的一个,只讨论两种就可以了,不必对四种命题形式-一加以讨论.
思考2? 观察上面5个例子中的原命题、逆命题、否命题以及逆否命题,你能说出每个例子中的四种命题的真假性有几种情况吗?
结合上面的5个实例和思考2,你能从中发现四种命题的真假性间有什么规律吗?
知识导读,由于原命题和它的逆否命题有相同的真假性,所以我们在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题。
22.(本小题满分12分)
已知 、B、C是椭圆M:
、B、C是椭圆M: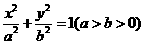 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为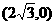 ,BC过椭圆M的中心,且
,BC过椭圆M的中心,且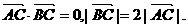
(1)求椭圆M的方程;
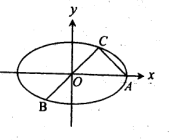 (2)过点
(2)过点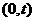 的直线
的直线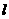 (斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与
(斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与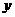 轴负半轴的交点,且
轴负半轴的交点,且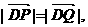 求实数
求实数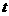 的取值范围。
的取值范围。
冀州中学08-09学年高二下学期升级考试(数学文)
21.(本小题满分12分)已知数列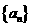 是首项为
是首项为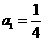 ,公比
,公比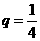 的等比数列,设
的等比数列,设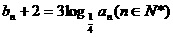 ,数列
,数列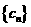 满足
满足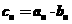 .
.
(Ⅰ)求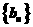 的通项公式;
的通项公式;
(Ⅱ)若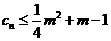 对一切正整数
对一切正整数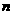 恒成立,求实数
恒成立,求实数 的 取值范围.
的 取值范围.
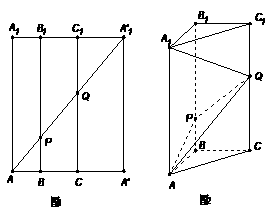
19.(本小题满分12分)
如图1所示,在边长为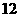 的正方形
的正方形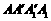 中,
中,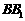
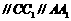 ,且
,且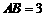 ,
,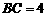 ,
,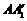 分别交
分别交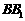
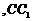 点于
点于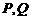 ,将该正方形沿
,将该正方形沿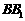 、
、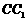 折叠,使得
折叠,使得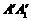 与
与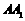 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱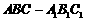 中
中
(Ⅰ)求证: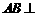
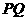 ;
;
(Ⅱ)在底边 上有一点
上有一点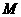 ,
,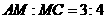 ,求证:
,求证: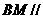 面
面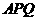
(III)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
20(12分)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量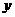 (升)关于行驶速度
(升)关于行驶速度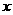 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: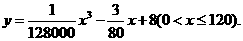 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com