
题目列表(包括答案和解析)
2.一元二次不等式:(1)解题步骤:① ② ③ ;
(2)“三个二次的关系”: ① ,
② ,③ ;
1.一元一次不等式: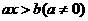 解集 ;
解集 ;
2.其它证明方法:反证法、判别式法、换元法、放缩法,构造函数法等
(1)反证法:“正难则反”,常用于唯一性、“至多、至少”性命题、否定或肯定性命题;
(2)判别式法:将多元不等式构造成 函数,再利用判别式符号证明;
(3)换元法:常用三角换元,若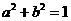 ,则可设
,则可设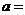 ,
,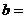 ,
,
若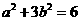 ,则可设
,则可设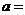 ,
,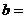 ;
;
(4)放缩法:技巧:①舍去或添加项
②放大或缩小分母,若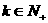 ,
,
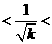 ,
, 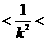 ,
,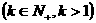 ③利用已知公式,如均值不等式,“加糖公式”;
③利用已知公式,如均值不等式,“加糖公式”;
(5) 构造函数法:构造函数,利用函数的单调性.
§6.4不等式的解法
各种类型的不等式解法:
1.证明不等式的三种基本方法: , , .
(1)比较法:作差、作商(先判断两式的符号);
(2)综合法:“由因导果”,常用到不等式的性质以及重要不等式;
(3)分析法:“执果索因”,各步可逆,
常用的化简方法有:平方、有理化、去分母等.
4.解决实际问题的步骤:(1)理解题意,设变量,一般把要求的最值设为函数;
(2)建立相应的函数关系式,把实际问题转化为求函数的最大、最小值问题;
(3)在定义域内利用均值不等式、对勾函数的单调性求最值;(4)写出正确答案.
§6.3不等式的证明
3.几个重要结论:
(1)函数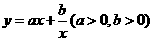 的单调性:
的单调性: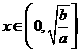 时函数 ,
时函数 ,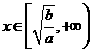 时函数 ,
时函数 ,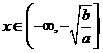 时函数 ,
时函数 ,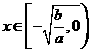 时函数 .
时函数 .
(2)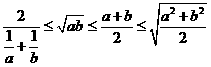 (当且仅当
(当且仅当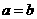 时取等号);
时取等号);
(3)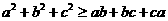 (当且仅当
(当且仅当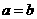 时取等号).
时取等号).
2.利用均值不等式求最值时,注意三点: ;
若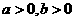 ,
,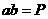 (定值),则
(定值),则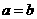 时
时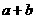 有最小值 (积定和最小);
有最小值 (积定和最小);
若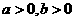 ,
,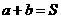 (定值),则
(定值),则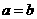 时
时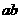 有最大值 (和定积最大)
有最大值 (和定积最大)
1.均值不等式:若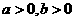 ,则
,则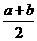
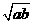 (当且仅当 时取等号).
(当且仅当 时取等号).
其中 为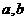 的算术平均数, 为
的算术平均数, 为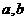 的几何平均数;
的几何平均数;
重要不等式: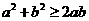 ,其中
,其中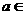 ,
,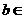 .
.
2.不等式的性质(请用“ ”或“
”或“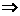 ”或“
”或“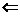 ”填空)
”填空)
(1)对称性: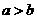
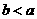 ;
;
(2)传递性: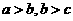
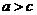 ,
,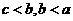
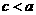 ;
;
(3)可加性: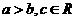
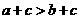 ,
,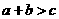
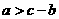 ,
,
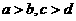
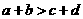 (同向不等式可以相加);
(同向不等式可以相加);
(4)可乘性: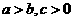
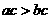 ,
,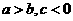
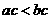 ,
,
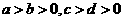
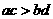 (同向正数不等式可以相乘);
(同向正数不等式可以相乘);
(5)乘方(开方)性质: 若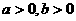 ,
,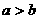
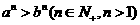 ,
,
若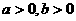 ,
,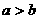
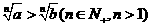 ;
;
(6)倒数性质: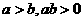
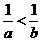 (同号的两个数大数的倒数反而小).
(同号的两个数大数的倒数反而小).
§6.2算术平均数与几何平均数
1.比较两数(两式)的大小常用作差法,步骤为(1) (2)
(3)
(4) ;变形时通常化成常数、几个平方和或因式乘积,采用的手段多为配方和因式分解.变形可能用到的公式有: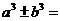
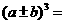 ,
,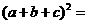 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com