
题目列表(包括答案和解析)
2、计算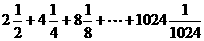 所得结果为( )
所得结果为( )
A.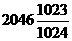 B.
B.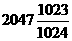 C.
C.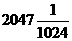 D.
D.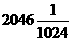
1、已知数列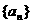 的前
的前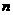 项和
项和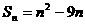 ,第
,第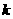 项满足
项满足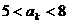 ,则
,则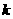 等于( )
等于( )
A. 6 B. 7 C.8 D. 9
2、非等差、等比数列的求和常用方法
(1)分组求和:通项虽不是等差、等比数列,但通过分组可化为由等差、等比的和的形式,如数列9,99,999,9999,…的前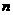 项和的计算
项和的计算
(2)裂项相消法:将通项表示为差的形式,求和时,中间若干项可正负相消,然后将保留的部分求和即可.举例分拆如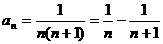 ,
,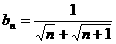
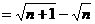
(3)错位相减法:等比数列求和公式推导过程的推广,此法适用于等差数列与等比数列乘积形式的数列求和.
1、 公式法求和
(1)
等差数列的前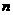 项和
项和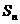 =__________=_____________
=__________=_____________
(2) 等比数列的前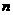 项和
项和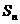 =_______________
=_______________
15. 解:(1)若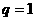 ,则
,则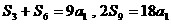 ,而
,而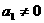 ,
,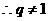
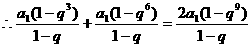 ,解得
,解得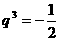 ,
,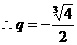
(2)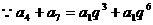
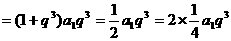
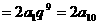
所以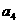 与
与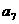 的等差中项是数列
的等差中项是数列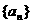 中的第10项
中的第10项
(3)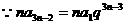
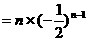
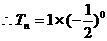
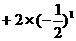
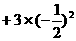
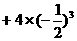
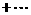
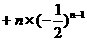 ………①
………①
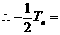
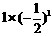
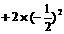
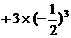
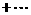
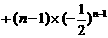
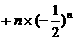 ……②
……②
①-②得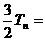
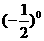
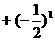
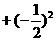
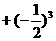
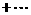
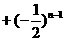
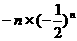
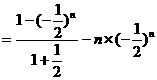
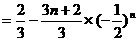
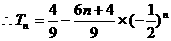
数列求和
14. 解:(1)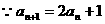 ,
,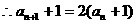
由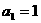 知
知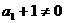 ,可得
,可得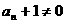
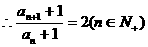 ,所以
,所以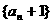 是等比数列
是等比数列
(2)由(1)得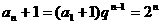 ,
,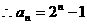
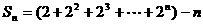 =
=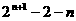
13. 解:因为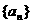 为等比数列,所以
为等比数列,所以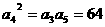 ,
,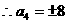
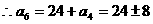 =32或16,又
=32或16,又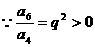 ,故
,故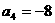 应舍去
应舍去
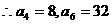 ,
,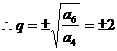
当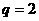 时,
时,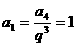 ,
,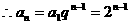 ,
,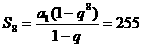
当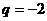 时,
时,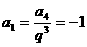 ,
,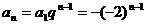 ,
,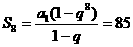
9.(1)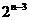 (2)6 10.
(2)6 10.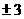 11.
11.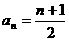 12.
12. 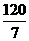
1. B 2. A 3. C 4. D 5. A 6. B 7. D 8. A
15、已知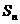 是等比数列
是等比数列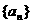 的前
的前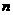 项和,
项和,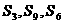 成等差数列.
成等差数列.
(1)求数列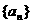 的公比
的公比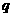 ;(2)试问
;(2)试问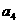 与
与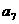 的等差中项是数列
的等差中项是数列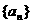 中的第几项?
中的第几项?
(3)若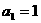 ,求数列
,求数列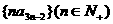 的前
的前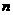 项和
项和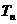 .
.
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com