
题目列表(包括答案和解析)
2、导数的四则运算法则:设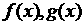 是可导的,则
是可导的,则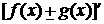
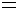 ;
;
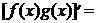 ,
,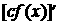
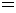 ;
;
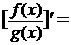 ,若
,若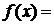 1,
1,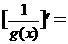 。
。
6.含有逻辑联结词的命题的否定:
(1) “ 或
或 ”的否定为:“
”的否定为:“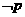 且
且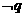 ”;
”;
(2) “ 且
且 ”的否定为:“
”的否定为:“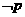 或
或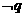 ”;
”;
(3) “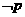 ”的否定为:“
”的否定为:“ ”.
”.
5.含有一个量词的命题的否定:
(1) “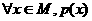 ”的否定为:“
”的否定为:“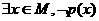 ”;
”;
(2) “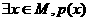 ”的否定为:“
”的否定为:“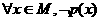 ”.
”.
4.复合命题真值表:
 |
 |
 或 或 |
 且 且 |
非 |
|
真 |
真 |
真 |
真 |
假 |
|
真 |
假 |
真 |
假 |
假 |
|
假 |
真 |
真 |
假 |
真 |
|
假 |
假 |
假 |
假 |
真 |
注:
(1) 且
且 为真
为真
 、
、 都真; (一假即假)
都真; (一假即假)
(2) 或
或 为假
为假
 、
、 都假; (一真即真)
都假; (一真即真)
(3)  为真命题,则
为真命题,则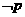 为假命题. (真假相反)
为假命题. (真假相反)
3.充要条件的判断:
(1)定义法:若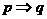 ,且
,且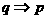 ,则
,则 是
是 充要条件.
充要条件.
(2)等价法:


(3)集合法:(集合 ,
, )
)
若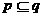 ,则
,则 是
是 的充分条件; 若
的充分条件; 若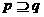 ,则
,则 是
是 的必要条件.
的必要条件.
若
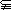
 ,则
,则 是
是 的充分不必要条件;若
的充分不必要条件;若

 ,则
,则 是
是 的必要不充分条件.
的必要不充分条件.
若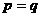 ,则
,则 是
是 的充要条件.
的充要条件.
2.充要条件:(记 表示条件,
表示条件, 表示结论)
表示结论)
(1)充分条件:若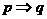 ,则
,则 是
是 充分条件.
充分条件.
(2)必要条件:若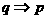 ,则
,则 是
是 必要条件.
必要条件.
若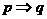 ,则
,则 是
是 的充分条件,反之,
的充分条件,反之, 是
是 的必要条件.
的必要条件.
(3)充要条件:若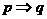 ,且
,且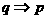 ,则
,则 是
是 充要条件.
充要条件.
(4)充分不必要条件:若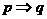 ,且
,且 ≠>
≠> ,则
,则 是
是 的充分不必要条件.
的充分不必要条件.
(5)必要不充分条件:若 ≠>
≠> ,且
,且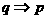 ,则
,则 是
是 的必要不充分条件.
的必要不充分条件.
(6)既不充分又不必要条件:若 ≠>
≠> ,且
,且 ≠>
≠> ,则
,则 是
是 的既不充分又不必要条件.
的既不充分又不必要条件.
1.

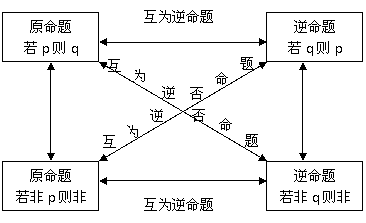 四种命题的相互关系:
四种命题的相互关系:
注:互为逆否命题的两个命题有相同的真假性.(即原命题 逆否命题,逆命题
逆否命题,逆命题 否命题)
否命题)
6.二次函数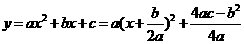
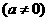 的图象是抛物线:
的图象是抛物线:
(1)顶点坐标为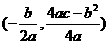 ;(2)对称轴
;(2)对称轴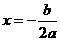 ;
;
(3)开口方向: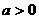 ,向上,
,向上, 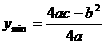
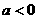 ,向下,
,向下,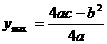
应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系
--二次方程
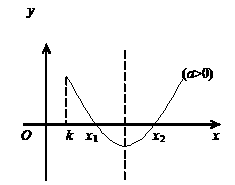
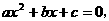
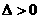 时,两根
时,两根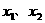 为二次函数
为二次函数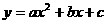 的图像与
的图像与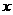 轴的两个焦点,也是二次不等式
轴的两个焦点,也是二次不等式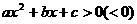 解集的端点值
解集的端点值
②求闭区间[m,n]上的最值。
③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题。
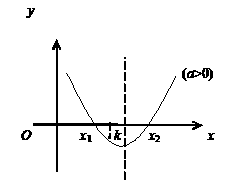 例如:二次方程
例如:二次方程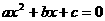 的两根都大于
的两根都大于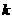
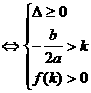
一根大于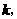 一根小于
一根小于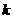
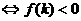
5.弦长公式: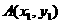 ,
,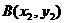 是抛物线上两点,则
是抛物线上两点,则
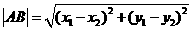
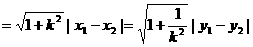
4.焦点弦的相关性质:焦点弦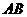 ,
,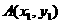 ,
,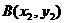 ,焦点
,焦点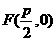
(1)以抛物线的焦点弦为直径的圆和抛物线的准线相切
(2) 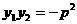 ,
,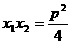
证明:①若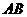 斜率不存在,则直线
斜率不存在,则直线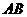 的方程为
的方程为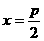 ,
,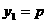 ,
,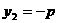 ∴
∴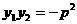
②若 斜率存在,记为
斜率存在,记为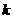 (
(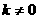 ),则
),则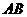 的方程为
的方程为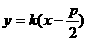
由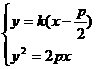 得
得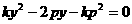 ∴
∴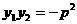 ,
,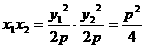 .
.
(3)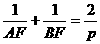
(4)通径:过焦点垂直于焦点所在的轴的焦点弦叫做通径.抛物线的通径长:2p.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com