
题目列表(包括答案和解析)
20.如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M、N分别是AB、PC的中点.
(1)求二面角P-CD-B的大小;
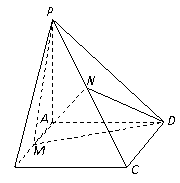 (2)求证:平面MND⊥平面PCD;
(2)求证:平面MND⊥平面PCD;
(3)求点P到平面MND的距离.
四川省遂宁市08-09学年高二下学期期末试卷
19.在某农场棉花试验基地,抽样测得某品种棉花纤维的纤度(表示纤维粗细的一种量)共有100个数据,将这些数据分组如右表:
(1)请补全答卷上的频率分布表和频率分布直方图;
(2)估计纤度落在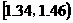 中的概率及纤度不小于1.42的概率是多少?
中的概率及纤度不小于1.42的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如,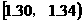 的中点值是1.32)作为代表,据此,估计这块棉花试验基地的棉花纤维纤度的平均值(结果精确到0.01).
的中点值是1.32)作为代表,据此,估计这块棉花试验基地的棉花纤维纤度的平均值(结果精确到0.01).
18.2009年6月2日,《食品安全法》正式公布实施,最引人注目的是取消了“食品免检”.某品牌食品在进入市场前必须对四项指标依次进行检测.如果四项指标中的第四项不合格或其他三项中的两项不合格,则该品牌食品不能进入市场.已知每项检测是相互独立的,且前三项指标不合格的概率均是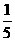 .
.
(1)求恰在第三项指标检测结束时,能确定该食品不能进入市场的概率;
|
分组 |
频数 |
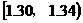 |
4 |
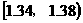 |
16 |
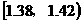 |
32 |
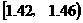 |
24 |
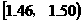 |
16 |
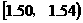 |
8 |
|
合计 |
100 |
(2)求在第三项指标检测结束时,还不能确定该品牌食品能否进入市场的概率.
17.如图,正三棱柱ABC-A1B1C1的各条棱长均为a,E、F、G分别是AC、AB、AA1的中点.
(1)请在图中作出过BC且平行于平面EFG的一个截面,并说明理由;
(2)求所作截面图形的面积.
16.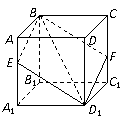 如图所示,在正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,给出下列四个结论:
如图所示,在正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,给出下列四个结论:
①四边形BFD1E一定是平行四边形;
②四边形BFD1E有可能是正方形;
③四边形BFD1E在底面ABCD内的投影一定是正方形;
④平面BFD1E有可能垂直于平面ABB1A1.
其中正确的结论有__________.(写出所有正确结论的编号)
15.在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有_________种.(用数字作答)
14.口袋内有100个大小相同的红球、白球和黑球,其中有45个红球,从中摸出一个球,摸出白球的概率是0.23,那么摸出黑球的概率是__________.
13.某校高二年级有男生500名,女生400名,为了解该年级男女生的健康状况,现采用分层抽样的方法抽取了25名男生,则应抽取女生_________名.
12.正三角形ABC的边长为a,P、Q分别是AB、AC上的点,PQ//BC,沿PQ将△ABC折起,使平面APQ⊥平面BPQC,设折叠后A、B两点间的距离为d,则d的最小值为
A.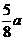 B.
B.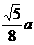 C.
C.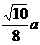 D.
D.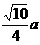
第Ⅱ卷(非选择题,共52分)
11. 底面边长为2的正三棱锥P-ABC中,E是BC的中点,若△PAE的面积为
底面边长为2的正三棱锥P-ABC中,E是BC的中点,若△PAE的面积为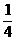 ,则侧棱PA与底面所成角的正切值是
,则侧棱PA与底面所成角的正切值是
A.1 B.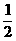 C.
C.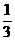 D.
D.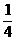
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com