
题目列表(包括答案和解析)
1、若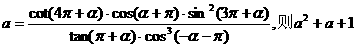 的值等于 (
)
的值等于 (
)
A.1 B.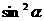 C.
C.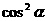 D.3
D.3
10、解:(1)以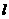 为
为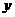 轴,且点
轴,且点 在
在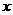 轴的正半轴上建立直角坐标系,则
轴的正半轴上建立直角坐标系,则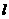 的方程为
的方程为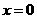 ,
,
点 的坐标为
的坐标为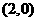 ,设点
,设点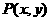 是曲线段
是曲线段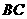 上任意一点,则
上任意一点,则
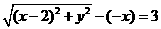 ,
,
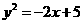
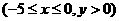 .………..4分
.………..4分
(2)设点
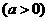 ,点
,点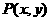 是曲线段
是曲线段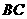 上任意一点,依题意:
上任意一点,依题意:
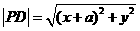
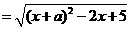
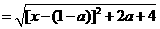 ,…….6分
,…….6分
若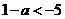 即
即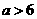 ,则当
,则当 时,
时, ;………..8分
;………..8分
若 即
即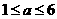 ,则当
,则当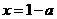 时,
时,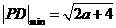 ;……….10分
;……….10分
若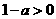 即
即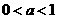 ,则当
,则当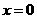 时,
时,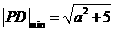 .………..12分
.………..12分
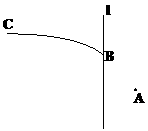
10、如图所示,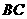 是一条曲线段,点
是一条曲线段,点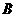 在直线
在直线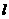 上。点
上。点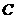 到
到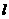 的距离等于5,
的距离等于5,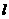 外一点
外一点 到
到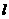 的距离为2。对于曲线段
的距离为2。对于曲线段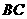 上的任意一点
上的任意一点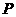 ,总满足
,总满足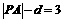 ,其中
,其中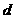 是点
是点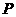 到直线
到直线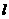 的距离.
的距离.
 (Ⅰ)建立适当的坐标系,求出曲线段
(Ⅰ)建立适当的坐标系,求出曲线段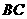 的方程; (Ⅱ)设另有一定点
的方程; (Ⅱ)设另有一定点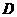 ,
,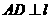 ,
, 、
、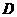 位于
位于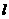 的两侧,且点
的两侧,且点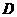 到
到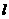 的距离为
的距离为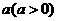 ,求曲线段
,求曲线段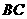 上的点到点
上的点到点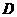 的最近距离.
的最近距离.
作业(12)答案:1、C 2、D 3、A 4、A 5、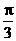 6、67 7、
6、67 7、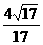 8、256,
8、256,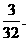
9:解:(1)由已知得f (n)=f (n -1) f (1)=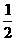 f (n-1)=
f (n-1)=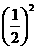 f (n-2)=…=
f (n-2)=…=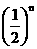 ;….4分
;….4分
(2)由(1)知 ,设
,设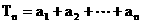 ,则用错位相减法求和得:
,则用错位相减法求和得:
 ;……..9分
;……..9分
(3)∵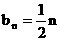 ∴
∴ 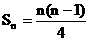
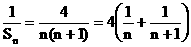
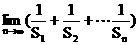 = 4
= 4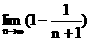 = 4.……………….12分
= 4.……………….12分
9、已知函数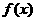 满足
满足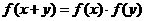 ,且
,且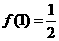 . (1)当
. (1)当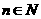 时,求
时,求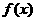 的表达式;
(2)设
的表达式;
(2)设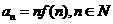 ,求证:
,求证: ;
;
(3)设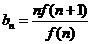 ,
,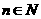 ,
,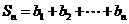 ,求
,求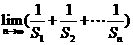 .
.
8、已知集合S=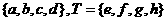 ,则从S到T的函数有 个,且存在反函
,则从S到T的函数有 个,且存在反函
数的概率为 ..
7、锥体体积V可以由底面积S与高h求得: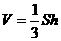 . 已知正三棱锥P-ABC底面边长为2
. 已知正三棱锥P-ABC底面边长为2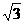 ,体积为4
,体积为4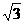 ,则底面三角形ABC的中心O到侧面PAB的距离为
.
,则底面三角形ABC的中心O到侧面PAB的距离为
.
6、已知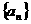 的前n项和
的前n项和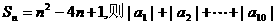 =
.
=
.
5、已知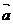 =(sinA,cosA),
=(sinA,cosA),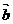 =(cosC,sinC),若
=(cosC,sinC),若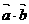 =sin2B,且A、B、C为三角形的内角B= .
=sin2B,且A、B、C为三角形的内角B= .
4、设A、B是非空集合,定义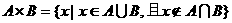 ,已知
,已知
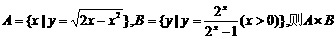 等于 ( )
等于 ( )
A.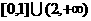 B.
B.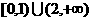 C.[0,1] D.[0,2]
C.[0,1] D.[0,2]
3、双曲线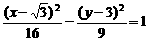 的焦点到渐近线的距离为 ( )
的焦点到渐近线的距离为 ( )
A.2 B.3 C.4 D.5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com