
题目列表(包括答案和解析)
11已知曲线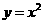 ,则过点
,则过点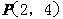 的切线方程为
的切线方程为 ;已知曲线
;已知曲线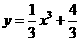 ,则过点
,则过点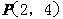 的切线方程为
的切线方程为 。
。
12若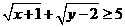 ,则
,则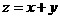 的最小值等于
的最小值等于 。
。
13设 ,若
,若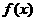 的图像向左平移至少
的图像向左平移至少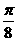 个长度单位后得到的图像恰为奇函数的图像,而向右平移至少
个长度单位后得到的图像恰为奇函数的图像,而向右平移至少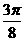 个长度单位后得到的图像恰为偶函数的图像,则
个长度单位后得到的图像恰为偶函数的图像,则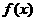 的最小正周期为
的最小正周期为 。
。
14将一个侧棱互不相等的四棱锥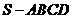 的每个顶点染上一种颜色,并使同一条棱的两个端点异色,如果只有5种颜色可供,那么不同的染色方法种数为
的每个顶点染上一种颜色,并使同一条棱的两个端点异色,如果只有5种颜色可供,那么不同的染色方法种数为 。
。
15给出命题:①圆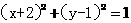 关于点
关于点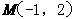 对称的圆方程为
对称的圆方程为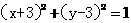 ;②双曲线
;②双曲线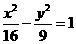 右支上一点P到左准线距离为18,则该点到右焦点距离为
右支上一点P到左准线距离为18,则该点到右焦点距离为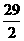 ;③顶点在原点,对称轴为坐标轴,且过
;③顶点在原点,对称轴为坐标轴,且过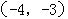 的抛物线方程只能是
的抛物线方程只能是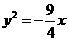 ;④
;④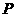 、
、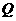 是椭圆
是椭圆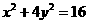 上两个动点,
上两个动点, 为坐标原点,直线
为坐标原点,直线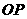 、
、 的斜率之积为
的斜率之积为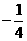 ,则
,则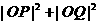 等于定值20。把你认为正确的命题序号填写在横线上
等于定值20。把你认为正确的命题序号填写在横线上 。
。
16已知椭圆的离心率为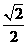 ,
,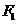 、
、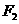 是两个焦点,
是两个焦点,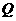 是椭圆上任意一点,则
是椭圆上任意一点,则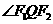 的最大值为
的最大值为 。
。
[ ]1已知: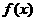 是R上的增函数,点
是R上的增函数,点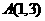 、
、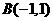 在它的图像上,
在它的图像上,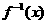 为其反函数,则不等式
为其反函数,则不等式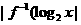 <1的解集是
<1的解集是
(A)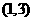 ;
(B)
;
(B)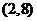 ; (C)
; (C)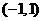 ;
(D)
;
(D)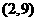 。
。
[ ]2定义在R上的函数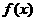 满足
满足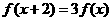 ,当
,当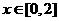 时,
时,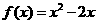 ,则当
,则当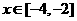 时,
时,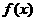 的最小值是(A)
的最小值是(A)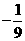 ;(B)
;(B)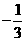 ;(C)
;(C)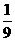 ;(D)
;(D)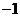 。
。
[ ]3设曲线 在
在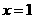 处的切线方程为
处的切线方程为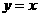 ,则
,则
(A)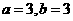 ;(B)
;(B)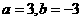 ;(C)
;(C)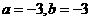 ;(D)
;(D)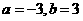 。
。
[ ]4已知数列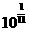 、
、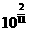 、
、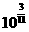 、……、
、……、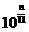 、……,它的前n项积大于
、……,它的前n项积大于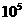 ,则正整数n的最小值为
(A)8; (B)10; (C)11; (D)12。
,则正整数n的最小值为
(A)8; (B)10; (C)11; (D)12。
[ ]5集合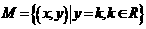 ,
,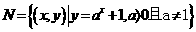 ,若
,若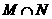 只有一个子集,则实数k的取值范围为
只有一个子集,则实数k的取值范围为
(A)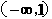 ; (B)
; (B)
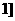 ; (C)
; (C)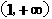 ; (D)
; (D)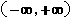 。
。
[ ]6有4位学生参加某种竞赛,竞赛规则规定:每位同学必须从甲、乙两题中任选一题作答,选甲答对得100分,答错得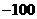 分;选乙答对得90分,答错得
分;选乙答对得90分,答错得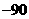 分。若4位同学的总分为0分,则这4位同学不同得分情况的种数是
分。若4位同学的总分为0分,则这4位同学不同得分情况的种数是
(A)48; (B)36; (C)24; (D)18。
[ ]7某班有48名学生,某次数学测验,算术平均分为70分,标准差为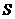 ,后发现成绩记录有误,某甲得80分却记为50分,某乙得70分却记为100分,更正后计算得标准差为
,后发现成绩记录有误,某甲得80分却记为50分,某乙得70分却记为100分,更正后计算得标准差为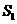 ,则
,则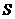 与
与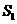 之间大小关系是
之间大小关系是
(A)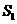 >
>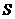 ; (B)
; (B)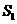
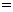
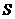 ;
(C)
;
(C)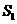 >
>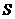
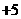 ; (D)
; (D)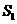 <
<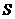 。
。
[ ]8四棱锥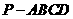 中,
中,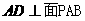 ,
, ,底面
,底面 为梯形,
为梯形,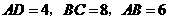 ,
,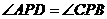 ,满足上述条件的四棱锥
,满足上述条件的四棱锥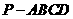 的顶点
的顶点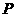 的轨迹是
的轨迹是
(A)圆; (B)不完整的圆; (C)抛物线; (D)抛物线的一部分。
[ ]9已知实数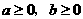 且
且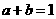 ,则
,则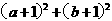 的取值范围为
的取值范围为
(A)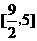 ; (B)
; (B)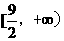 ; (C)
; (C)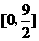 ;
(D)
;
(D)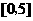 。
。
[ ]10 若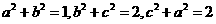 ,则
,则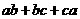 的最小值为
的最小值为
(A)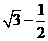 ; (B)
; (B)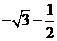 ; (C)
; (C)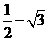 ; (D)
; (D)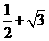 。
。
17 已知函数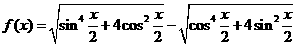 。
。
(Ⅰ)化简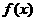 并求
并求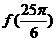 的值;
的值;
(Ⅱ)若0<α<π,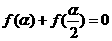 求α。
求α。
18如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,
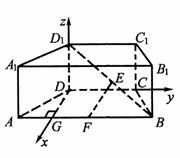 AB=2AD=2DC=2,E为BD1的中点,F为AB的中点。
AB=2AD=2DC=2,E为BD1的中点,F为AB的中点。
(Ⅰ)求证:EF∥平面ADD1 A1;
(Ⅱ)建立空间直角坐标系D-xyz (DG是AB边上的高),若BB1=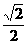 ,求A1F与平面DEF所成的角的大小。
,求A1F与平面DEF所成的角的大小。
19已知椭圆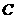 的中心在原点,焦点在
的中心在原点,焦点在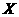 轴上,一条经过点
轴上,一条经过点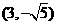 ,方向为
,方向为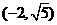 的直线
的直线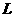 交椭圆于
交椭圆于 、
、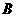 两点,交
两点,交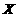 轴于
轴于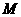 点,又
点,又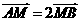 。
。
(Ⅰ)求直线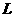 的方程;
的方程;
(Ⅱ)求椭圆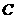 的长轴长的取值范围。
的长轴长的取值范围。
20已知定义在R上的函数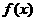 满足:对于任意实数x, y ,恒有
满足:对于任意实数x, y ,恒有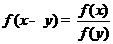 ,且当x>0时,
,且当x>0时,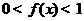 。
。
(Ⅰ)求证: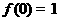 且当x<0时,有
且当x<0时,有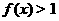 ;
;
(Ⅱ)试判断函数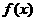 在R上的单调性,并证明你的结论;
在R上的单调性,并证明你的结论;
(Ⅲ)若实数x、y满足: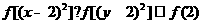 且
且 求z=x+y取值范围。
求z=x+y取值范围。
21在直角坐标平面上有一点列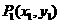 、
、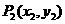 、…、
、…、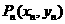 、…,对每个正整数
、…,对每个正整数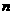 ,点
,点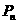 位于函数
位于函数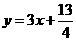 图像上,且
图像上,且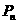 横坐标构成以
横坐标构成以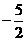 为首项,
为首项,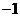 为公差的等差数列
为公差的等差数列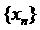 。
。
(Ⅰ)设抛物线 、
、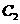 、
、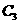 、…,
、…, 、…中的每一条的对称轴都垂直于
、…中的每一条的对称轴都垂直于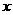 轴,第
轴,第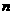 条抛物线
条抛物线 的顶点为
的顶点为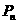 且过点
且过点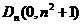 ,记过点
,记过点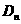 且与抛物线
且与抛物线 只有一个交点的直线的斜率为
只有一个交点的直线的斜率为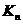 ,求证:
,求证: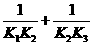 +…
+…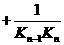 <
<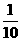 ;
;
(Ⅱ)设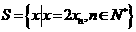 ,
,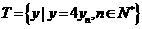 ,等差数列
,等差数列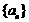 的任一项
的任一项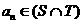 ,其中
,其中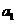 是
是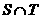 中的最大数,
中的最大数,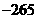 <
<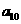 <
<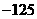 ,求
,求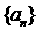 通项公式。
通项公式。
11已知函数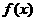 是区间
是区间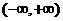 上的减函数,且满足
上的减函数,且满足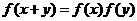 ,
,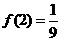 ,则不等式
,则不等式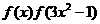 <
<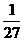 的解集为
的解集为 。
。
12王大鹏每天骑自行车上学,从他家到学校的途中要过4个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的且概率均为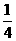 ,则他连续在两个交通岗遇到红灯的概率为
,则他连续在两个交通岗遇到红灯的概率为 。
。
13已知函数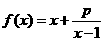 (x>1,p为正常数)与
(x>1,p为正常数)与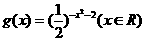 有相同的值域,则
有相同的值域,则 的值为
的值为 。
。
14将正整数排成下表:1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
如果将第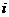 行第
行第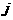 列的那个数记为
列的那个数记为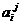 ,则数表中的2008就记为
,则数表中的2008就记为 。
。
15设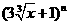 的展开式中各项系数之和为A,各项的二项式系数之和为B,如果
的展开式中各项系数之和为A,各项的二项式系数之和为B,如果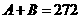 ,则展开式中x的系数为
,则展开式中x的系数为 。
。
16计算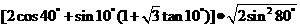
 。
。
[ ]1称集合 的非空真子集的真子集叫做集合
的非空真子集的真子集叫做集合 的“孙子集”,则集合
的“孙子集”,则集合 ={1,2,3,4,5}的孙子集共有
={1,2,3,4,5}的孙子集共有
(A)11个; (B)39个; (C)26个; (D)10个。
[ ]2各项均为实数的等比数列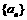 的前n项和为
的前n项和为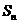 ,若
,若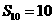 ,
,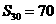 ,则
,则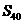 等于
(A)150;
(B)
等于
(A)150;
(B)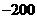 ; (C)150或
; (C)150或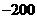 ; (D)400或
; (D)400或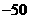 。
。
[ ]3设函数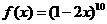 ,则导函数
,则导函数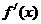 的展开式中
的展开式中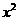 项的系数为
项的系数为
(A)1440;
(B)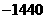 ; (C)
; (C)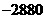 ; (D)2880。
; (D)2880。
[ ]4已知平面α及以下3个几何体:①长、宽、高皆不相等的长方体;②底面为平行四边形但不是矩形的四棱锥;③正四面体。这3个几何体在平面上的射影可以是正方形的是
(A)①②③; (B)①②; (C)①③; (D)②③。
[ ]5已知两个点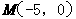 、
、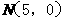 ,若直线上存在点P,使
,若直线上存在点P,使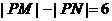 ,则称该直线为“B型直线”,给出下列直线①
,则称该直线为“B型直线”,给出下列直线①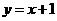 ,②
,②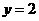 ,③
,③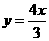 ,④
,④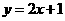 。其中为“B型直线”的是
。其中为“B型直线”的是
(A)①③; (B)①②; (C)③④; (D)①④。
[ ]6已知函数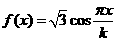 ,若经过该函数图像上的一个最大值点与一个最小值点的直线的最大斜率等于
,若经过该函数图像上的一个最大值点与一个最小值点的直线的最大斜率等于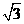 ,则
,则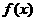 的最小正周期为
的最小正周期为
(A)1; (B)2; (C)3; (D)4。
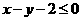
[ ]7设实数x、y满足不等式 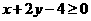 ,则
,则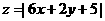 的最小值为
的最小值为
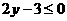
(A)14;
(B)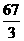 ; (C)29;
(D)不存在。
; (C)29;
(D)不存在。
[
]8已知函数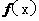 的反函数
的反函数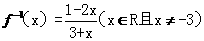 ,则
,则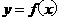 的图形
的图形
(A)关于点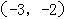 对称;
(B)关于点
对称;
(B)关于点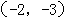 对称;
对称;
(C)关于直线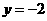 对称;
(D)关于直线
对称;
(D)关于直线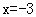 对称。
对称。
[ ]9点P是椭圆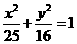 上的一点,
上的一点,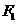 、
、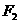 是其两焦点,且△
是其两焦点,且△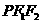 的内切圆半径是1,则当P在第一象限时,它的纵坐标是
的内切圆半径是1,则当P在第一象限时,它的纵坐标是
(A)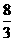 ;
(B)
;
(B)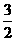 ; (C)
; (C)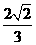 ; (D)
; (D)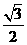 。
。
[ ]10已知关于m的方程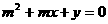 有两个绝对值都不大于1的实数根,设点
有两个绝对值都不大于1的实数根,设点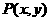 是坐标平面内所对应的区域内的动点,则
是坐标平面内所对应的区域内的动点,则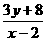 取值范围是
取值范围是
(A)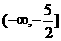 ;
(B)
;
(B)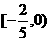 ; (C)
; (C)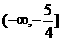 ;
(D)
;
(D)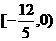 。
。
20.(本题满分14分)
对于函数y=f(x),若同时满足下列条件:
① 函数y=f(x)在定义域D内是单调递增或单调递减函数;
② 存在区间[a,b] D,使函数f(x)在[a,b]上的值域为[a,b],则称f(x)是D上的闭函数.
D,使函数f(x)在[a,b]上的值域为[a,b],则称f(x)是D上的闭函数.
(1) 求闭函数f(x)=-x3符合条件②的区间[a,b];
(2) 判断函数g(x)=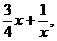 在区间(0,+∞)上是否为闭函数;
在区间(0,+∞)上是否为闭函数;
(3) 若函数φ(x)=k+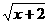 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
19. (本题满分14分)
已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2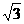 .
.
(1) 求双曲线C的方程;
(2) 若直线l:y=kx+ 与双曲线C左支交于A、B两点,求k的取值范围;
与双曲线C左支交于A、B两点,求k的取值范围;
(3) 在(2)的条件下,线段AB的垂直平分线l0与y轴交于M(0,b),求b的取值范围.
18.(本题满分12分)
等比数列{xn}各项均为正值,yn=2logaxn(a>0且a≠1,n∈N*),已知y4=17,y7=11.
(1) 求证:数列{yn}是等差数列;
(2) 数列{yn}的前多少项的和为最大?最大值为多少?
(3) 当n>12时,要使xn>2恒成立,求a的取值范围.
17.(本题满分13分)
某汽车在前进途中要经过4个路口,但由于路况不同,汽车在前两个路口遇到绿灯的概率为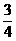 ,在后两个路口遇到绿灯的概率为
,在后两个路口遇到绿灯的概率为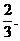 假定汽车只在遇到红灯或到达目的地时才停止前进,ξ表示停车时已经通过的路口数,求:
假定汽车只在遇到红灯或到达目的地时才停止前进,ξ表示停车时已经通过的路口数,求:
(1) 停车时已通过2个路口的概率;
(2) 停车时至多已通过3个路口的概率;
(3) ξ的概率分布列,数学期望Eξ.
16. (本题满分14分)
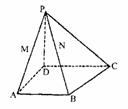 在四棱锥P-ABCD中,AB⊥CD,CD∥AB,PD⊥底面ABCD,AB=
在四棱锥P-ABCD中,AB⊥CD,CD∥AB,PD⊥底面ABCD,AB= AD,直线PA与底面ABCD成60°角,M、N分别是PA、PB的中点.
AD,直线PA与底面ABCD成60°角,M、N分别是PA、PB的中点.
(1) 求证:直线MN∥平面PDC;
(2) 若∠CND=90°,求证:直线DN⊥直线PC;
(3) 求二面角P-MN-D的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com