
题目列表(包括答案和解析)
2、已知过点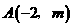 和
和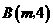 的直线与直线
的直线与直线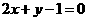 平行,则的值为 ( )
平行,则的值为 ( )
A  B
B 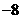 C
C 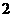 D
D 
1、 已知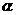 为第三象限的角,则
为第三象限的角,则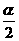 所在的象限是( )
所在的象限是( )
A 第一或第二象限 B 第二或第三象限 C第一或第三象限 D 第二或第四象限
(17)(本小题满分12分)
已知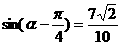 ,
,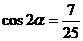 ,求sina及
,求sina及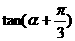

(18)(本小题满分12分)
若公比为c的等比数列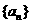 的首项
的首项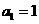 且满足
且满足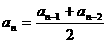 (n3,4,…)
(n3,4,…)
(Ⅰ)求c的值;
(Ⅱ)求数列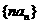 的前n项和
的前n项和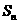

(19)(本小题满分12分)
如图,在斜三棱柱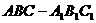 中,
中,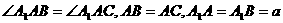 ,侧面
,侧面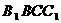 与底面ABC所成的二面角为
与底面ABC所成的二面角为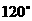 ,E、F分别是棱
,E、F分别是棱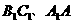 的中点
的中点
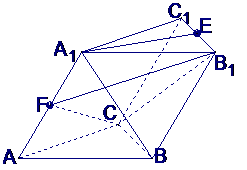 (Ⅰ)求
(Ⅰ)求 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明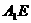 ∥平面
∥平面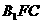
(Ⅲ)求经过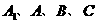 四点的球的体积
四点的球的体积
 (20)(本小题满分12)
(20)(本小题满分12)
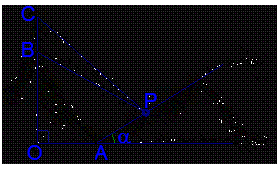
某人在一山坡P处观看对面山项上的一座铁塔 如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC80(米),山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,
如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC80(米),山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,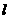 与水平地面的夹角为a,
与水平地面的夹角为a,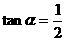 ,试问,此人距山崖的水平地面多高时,观看塔的视角ÐBPC最大(不计此人的身高)?
,试问,此人距山崖的水平地面多高时,观看塔的视角ÐBPC最大(不计此人的身高)?
(21)(本小题满分14分)
已知mÎR,设P: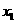 和
和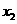 是方程
是方程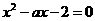 的两个实根,不等式
的两个实根,不等式
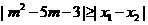 对任意实数
对任意实数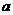 Î[-1,1]恒成立;
Î[-1,1]恒成立;
Q:函数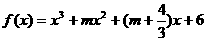 在(-¥,+¥)上有极值
在(-¥,+¥)上有极值
求使P正确且Q正确的m的取值范围
(22)(本小题满分14分)
抛物线C的方程为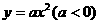 ,过抛物线C上一点P(x0,y0)(x0¹0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x0¹0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点互不相同),且满足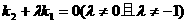

(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足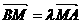 ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当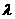 1时,若点P的坐标为(1,1),求ÐPAB为钝角时点A的纵坐标
1时,若点P的坐标为(1,1),求ÐPAB为钝角时点A的纵坐标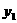 的取值范围
的取值范围
2005年高考文科数学 天津卷
天津卷 试题及答案
试题及答案
(11)二项式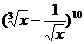 的展开式中常数项为__________(用数字作答).
的展开式中常数项为__________(用数字作答).
 (12)已知
(12)已知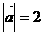 ,
,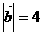 ,
,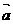 与
与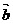 的夹角为
的夹角为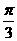 ,以
,以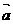 ,
,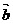 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为__________
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为__________
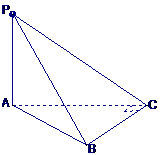
(13) 如图,PA⊥平面ABC,∠ACB=90°且PA=AC=BC=a则异面直线PB与AC所成角的正切值等于________.
(14)在数列{an}中,a11,a22,且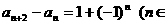 N*)则S10__________
N*)则S10__________
 (15)设函数
(15)设函数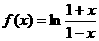 ,则函数
,则函数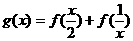 的定义域为__________
的定义域为__________
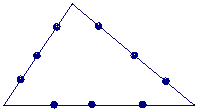
(16)在三角形的每条边上各取三个分点(如图) 以这9个分点为顶点可画出若干个三角形
以这9个分点为顶点可画出若干个三角形 若从中任意抽取一个三角形,则其三个顶点分别落在原三角形的三条不同边上的概率为__________(用数字作答)
若从中任意抽取一个三角形,则其三个顶点分别落在原三角形的三条不同边上的概率为__________(用数字作答)
(1)设集合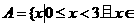 N}的真子集的个数是( )
N}的真子集的个数是( )
(A) 16 (B) 8; (C) 7 (D) 4
(2)已知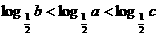 ,则( )
,则( )
(A) 2b>2a>2c; (B) 2a>2b>2c; (C) 2c>2b>2a (D) 2c>2a>2b
(3)某人射击一次击中的概率为0.6,经过3次射击,此人恰有两次击中目标的概率为( )
(A)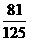 (B)
(B)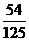 (C)
(C)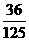 (D)
(D)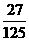
(4)将直线2xyl0沿x轴向左平移1个单位,所得直线与圆x2y22x4y0相切,则实数l的值为
(A) 3或7 (B) 2或8 (C) 0或10 (D) 1或11
(5)设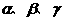 为平面,
为平面,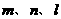 为直线,则
为直线,则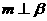 的一个充分条件是( )
的一个充分条件是( )
(A) 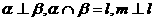 (B)
(B)
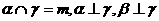
(C) 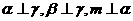 (D)
(D)
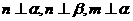
(6)设双曲线以椭圆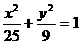 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为( )
(A)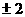 (B)
(B)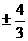 (C)
(C)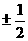 (D)
(D)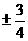
(7)给出下列三个命题:①若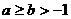 ,则
,则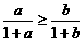 ;②若正整数
;②若正整数 和
和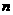 满足
满足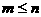 ,则
,则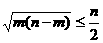 ;③设
;③设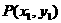 为圆
为圆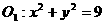 上任一点,圆
上任一点,圆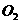 以
以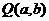 为圆心且半径为1.当
为圆心且半径为1.当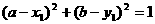 时,圆
时,圆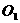 与圆
与圆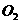 相切
相切
其中假命题的个数为( )
(A) 0 (B) 1 (C) 2 (D)3
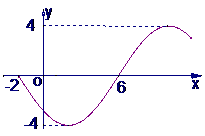 (8)函数yA(sinwxj)(w>0,
(8)函数yA(sinwxj)(w>0,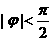 ,xÎR)的部分图象如图所示,则函数表达式为 ( )
,xÎR)的部分图象如图所示,则函数表达式为 ( )
(A) 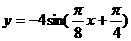
(B) 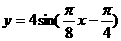
(C) 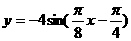
(D) 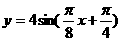
(9)若函数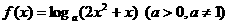 在区间
在区间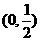 内恒有f(x)>0,则f(x)的单调递增区间为( )
内恒有f(x)>0,则f(x)的单调递增区间为( )
(A)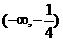 (B)
(B) 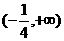
(C) (0,¥) (D) 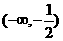
(10)设f(x)是定义在R上以6为周期的函数,f(x)在(0,3)内单调递增,且yf(x)的图象关于直线x3对称,则下面正确的结论是( )
(A) f(1.5)<f(3.5)<f(6.5) (B) f(3.5)<f(1.5)<f(6.5)
(C) f(6.5)<f(3.5)<f(1.5) (D) f(3.5)<f(6.5)<f(1.5)
第Ⅱ卷 (非选择题 共100分)
22.(本小题满分14分)
已知椭圆的中心为坐标原点O,焦点在x轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,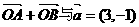 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且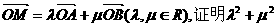 为定值.
为定值.
2005年普通高等学校招生全国统一考试
21.(本小题满分12分)
设正项等比数列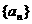 的首项
的首项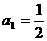 ,前n项和为Sn,且
,前n项和为Sn,且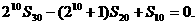
(Ⅰ)求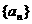 的通项;
的通项;
(Ⅱ)求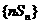 的前n项和Tn.
的前n项和Tn.
20.(本小题满分12分)
9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为0.5. 若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种.
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率.
(精确到0.001)
19.(本小题满分12分)
已知二次函数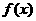 的二次项系数为a,且不等式
的二次项系数为a,且不等式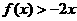 的解集为(1,3).
的解集为(1,3).
(1)若方程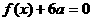 有两个相等的根,求
有两个相等的根,求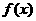 的解析式;
的解析式;
(2)若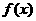 的最大值为正数,求a的取值范围.
的最大值为正数,求a的取值范围.
18.(本小题满分12分)
已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,
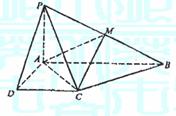 且
且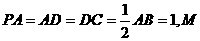 是PB的中点.
是PB的中点.
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com