
题目列表(包括答案和解析)
6、要得到函数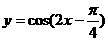 的图象,且使平移的距离最短,则需将函数
的图象,且使平移的距离最短,则需将函数
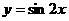 的图象
的图象
A、向左平移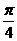 个单位
B、向右平移
个单位
B、向右平移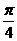 个单位
个单位
C、向左平移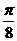 个单位
D、向右平移
个单位
D、向右平移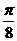 个单位
个单位
5、已知双曲线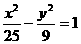 的左支上一点M到右焦点F1的距离为18,点N是MF1的中点,O为坐标原点,则|ON|等于
的左支上一点M到右焦点F1的距离为18,点N是MF1的中点,O为坐标原点,则|ON|等于
A、4 B、2 C、1 D、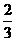
4、已知函数f(x)为奇函数,并且对任意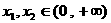 ,当
,当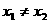 时,恒有
时,恒有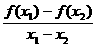 >0,则
>0,则
A、f(3)>f(-5) B、f(-3)<f(-5) C、f(-5)>f(3) D、f(-3)>f(-5)
3、某人射击命中目标的概率为0.6,每次射击互不影响,连续射击3次,至少有2次命中目标的概率为
A、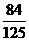 B、
B、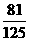 C、
C、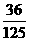 D、
D、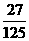
2、已知全集为U,若集合M、N是U的真子集,且同时满足: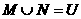 ,
,
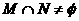 ,则下列关系式不成立的是
,则下列关系式不成立的是
A、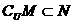 B、
B、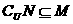 C、
C、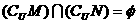 D、
D、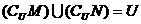
1、已知两点P(4,-9)、Q(-2,3),则直线PQ与y轴的交点分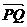 的比为
的比为
A、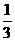 B、
B、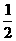 C、2 D、3
C、2 D、3
10、解:(I)设C、D点的坐标分别为C(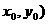 ,D
,D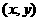 ,则
,则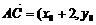 ),
),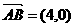 则
则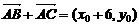 ,故
,故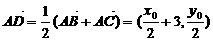 2分
2分
又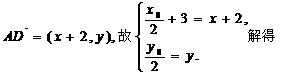
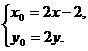 …………4分
…………4分
代入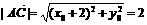 得
得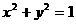 ,即为所求点D的轨迹方程.…………7分
,即为所求点D的轨迹方程.…………7分
(II)易知直线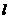 与
与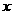 轴不垂直,设直线
轴不垂直,设直线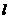 的方程为
的方程为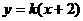 ①.
①.
又设椭圆方程为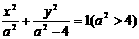 ②.
②.
因为直线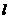 与圆
与圆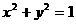 相切.故
相切.故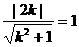 ,解得
,解得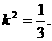
将①代入②整理得,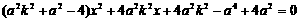 ,
,
而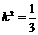 ,即
,即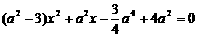 ,
,
设M( ,N(
,N(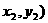 ,则
,则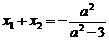 ,
,
由题意有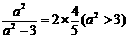 ,求得
,求得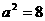 .经检验,此时
.经检验,此时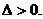
故所求的椭圆方程为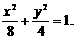 ……………14分
……………14分
9、解:(1)A中2张钱币取1张,有2种情况,B中3张钱币取1张,有3种情况,
∴互换一次有2×3=6情况.
其中10元币恰是一张的情况有3种,∴A袋中10元钱币恰是一张的概率为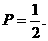 …………………………………………………………3分
…………………………………………………………3分
(2)A袋中恰有一张10元币的概率为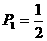 ;恰有两张10元币的概率为
;恰有两张10元币的概率为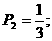 …………………………………………………………………………3分
…………………………………………………………………………3分
∴A袋中10元钱币至少是一张的概率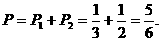 答略……3分
答略……3分
另解:A袋中恰有0张10元币的概率为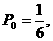 ……………………3分
……………………3分
∴A袋中10元钱币至少是一张的概率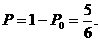 答略………………3分
答略………………3分
10、已知A(-2,0)、B(2,0),点C、点D满足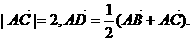
(1)求点D的轨迹方程;
(2)过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为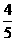 ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.
作业(9)答案:1、A 2、B 3、B 4、C 5、5 6、102 7、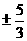 8、
8、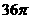
9、A袋中有1张10元1张5元的钱币,B袋中有2张10元1张5元的钱币,从A袋中任取一张钱币与B袋任取一张钱币互换,这样的互换进行了一次. (1)A袋中10元钱币恰是一张的概率; (2)A袋中10元钱币至少是一张的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com