
题目列表(包括答案和解析)
[答案]五、解:设 ,则
,则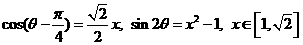
从而原不等式可化为:
即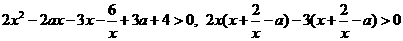 ,
,
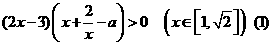
 原不等式等价于不等式(1)
原不等式等价于不等式(1)
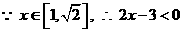
(1)不等式恒成立等价于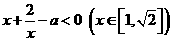 恒成立。
恒成立。
从而只要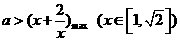 。
。
又容易知道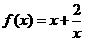 在
在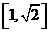 上递减,
上递减,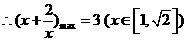 。
。
所以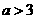 。
。
2004四年全国高中数学联合竞赛(天津初赛)
2.若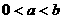 ,且
,且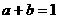 ,则下列各式中最大的是( C )
,则下列各式中最大的是( C )
(A)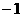 (B)
(B)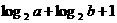
(C)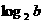 (D)
(D)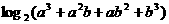
2004年全国高中数学联赛四川省初赛
22.(1)证明: 是以为.
是以为.
 (2).解:由(1)得
(2).解:由(1)得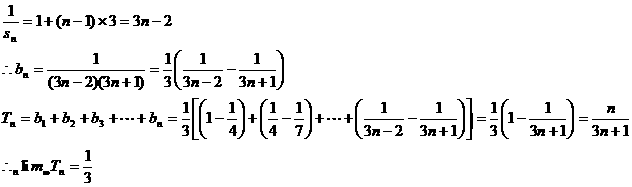
21. (1).解:由图可知a=5, c=4所以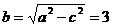 该椭圆的方程为
该椭圆的方程为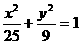
准线方程为
(2). 证明:设K点坐标为 (x0, 0) , 点P 。P1的坐标分别记为(x0, y0)、(x0, -y0) ,
其中0<x0<5则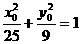 ① 直线A1P、P1A的方程分别为:
① 直线A1P、P1A的方程分别为: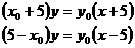

②式除以③式得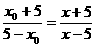 化简上式得
化简上式得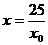 ,代入②式得
,代入②式得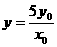 于是,
于是,
 直线A1P与AP1的交点M的坐标为
直线A1P与AP1的交点M的坐标为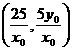
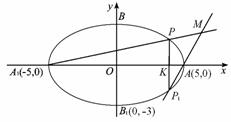
第21题图
因为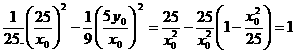 所以直线A1P与AP1的交点M在双曲线
所以直线A1P与AP1的交点M在双曲线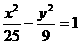 上。
上。
20.解:设事件Ai =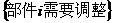 , I=1,2,3则
, I=1,2,3则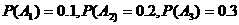 由题意, ξ可能有四个值0,1,2,3,由于各事件Ai相互独立,故
由题意, ξ可能有四个值0,1,2,3,由于各事件Ai相互独立,故
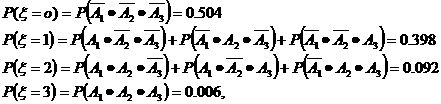
即
|
ξ |
0 |
1 |
2 |
3 |
|
P |
0.504 |
0.398 |
0.092 |
0.006 |
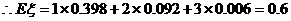
19.解:要使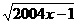 有意义,必须1-2004x≥0即x≤
有意义,必须1-2004x≥0即x≤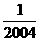 综合上述,必须
综合上述,必须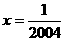 ,这时
,这时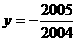 所以
所以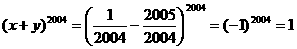
18. 解:(1)M、N分别是PB、OB的中点 M点的坐标为
M点的坐标为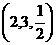 ,N点的坐标为
,N点的坐标为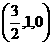 设R的坐标为(x1,y1,z1)
设R的坐标为(x1,y1,z1)
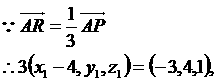
 R的坐标为
R的坐标为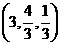


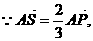 设S的坐标为
设S的坐标为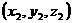

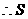 的坐标为
的坐标为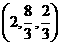

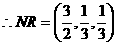

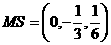

 设NR和MS之间的夹角为
设NR和MS之间的夹角为 ,
,



 则
则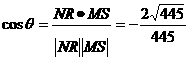
所以直线NR和MS的夹角的余弦值为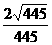
(2).设点P在平面xOy内的射影为点Q,则点Q的坐标为(1,4,0),点Q在OA上的射影D的坐标为(1,0,0)
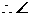 PDQ为二面角P-OA-B的平面角
PDQ为二面角P-OA-B的平面角


 DP=(0,4,1), DQ=(0,4,0)
DP=(0,4,1), DQ=(0,4,0)


 设DP与DQ间的夹角为
设DP与DQ间的夹角为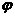 则
则




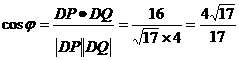
所求二面角的余弦值为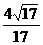 。
。
17.解(1)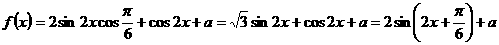
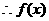 的最
的最 小正周期
小正周期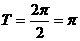
(2)当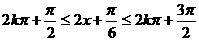 即
即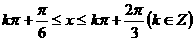 时,函数f(x)单调递减,故所求区间为
时,函数f(x)单调递减,故所求区间为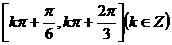
(3)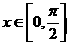 时,
时,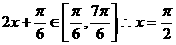 时,f(x)取得最小值
时,f(x)取得最小值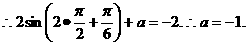
16.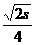
15.252
14.16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com