
题目列表(包括答案和解析)
18、(本小题满分13分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金a元,答对问题B可获奖金2a元;先答哪个题由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为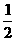 、
、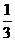 。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
17、(本小题满分13分)
已知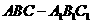 为正三棱柱,
为正三棱柱,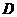 是
是 的中点.
的中点.
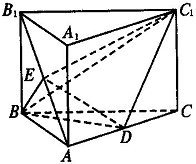 (1)证明:
(1)证明: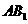 ∥平面
∥平面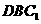
(2)若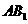 ⊥
⊥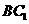 ,
,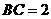
①求二面角D-BC1-C的大小;
②若E为AB1的中点,求三棱锥E-BDC1的体积。
16、(本小题满分13分)
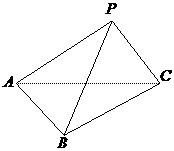 如图,三棱锥
如图,三棱锥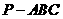 中,
中,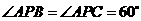 ,
,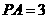 ,
,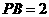 ,△
,△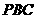 为正三角形,
为正三角形,
(Ⅰ)求证:平面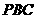 ⊥平面
⊥平面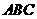 ;
;
(Ⅱ)求棱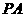 与侧面
与侧面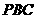 所成的角;
所成的角;
(Ⅲ)求点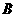 到侧面
到侧面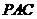 的距离。
的距离。
15、(本小题满分13分)
已知△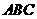 中,角A、B、C对应的边为a、b、c,A=2B,
中,角A、B、C对应的边为a、b、c,A=2B,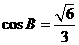 ,求sinC的值.
,求sinC的值.
14、已知 、
、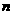 是直线,
是直线,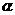 、
、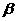 、
、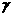 是平面,给出下列命题:
是平面,给出下列命题:
①
若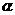 ⊥
⊥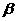 ,
,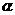 ∩
∩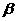 =
= ,
,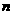 ⊥
⊥ ,则
,则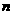 ⊥
⊥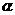 或
或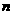 ⊥
⊥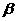 ;
;
②
若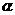 ∥
∥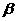 ,
,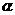 ∩
∩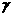 =
= ,
,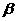 ∩
∩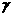 =
=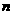 ,则
,则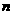 ∥
∥ ;
;
③
若 不垂直于
不垂直于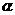 ,则
,则 不可能垂直于
不可能垂直于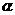 内的无数条直线;
内的无数条直线;
④
若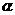 ∩
∩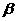 =
= ,
,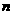 ∥
∥ ,且
,且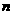
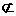
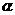 ,
,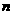
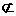
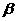 ,则
,则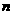 ∥
∥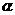 且
且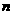 ∥
∥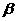 。
。
其中正确的命题的序号是 。(注:把你认为正确的命题序号都填上)
13、已知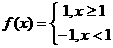 ,则不等式
,则不等式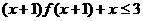 的解集是 。
的解集是 。
12、将时间拔慢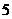 分钟,则分针转了 度,时针转了 度。
分钟,则分针转了 度,时针转了 度。
11、某校有教职工200人,男学生1000人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为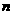 的样本,已知从教职工中抽取的人数为10,则
的样本,已知从教职工中抽取的人数为10,则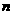 = 。
= 。
10、已知函数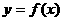 满足:①
满足:①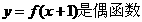 ;②在
;②在 上为增函数。若
上为增函数。若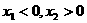 ,且
,且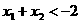 ,则
,则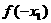 与
与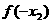 的大小关系是( )
的大小关系是( )
A、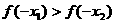 B、
B、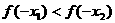
C、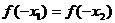 D、 无法确定
D、 无法确定
第Ⅱ卷(非选择题,共100分)
9、若无穷等比数列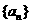 满足
满足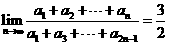 ,则数列的公比
,则数列的公比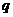 为( )
为( )
A、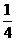 B、
B、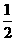 C、
C、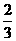 D、
D、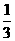
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com