
题目列表(包括答案和解析)
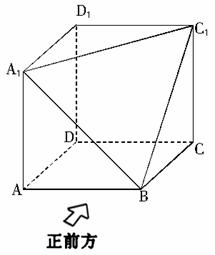
2、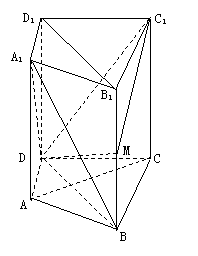 如图所示,在直四棱柱
如图所示,在直四棱柱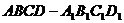 中,
中,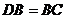 ,
, 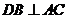 ,点
,点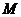 是棱
是棱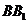 上一点.
上一点.
(1)求证: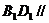 面
面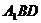 ;(2)求证:
;(2)求证: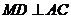 ;
;
(3)试确定点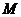 的位置,使得平面
的位置,使得平面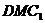
 平面
平面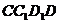 .
.
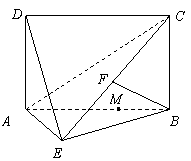
1、在几何体ABCDE中,∠BAC=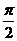 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
 (Ⅰ)求证:DC∥平面ABE;(Ⅱ)求证:AF⊥平面BCDE;(Ⅲ)求证:平面AFD⊥平面AFE.
(Ⅰ)求证:DC∥平面ABE;(Ⅱ)求证:AF⊥平面BCDE;(Ⅲ)求证:平面AFD⊥平面AFE.
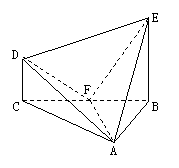
3、 直棱柱
直棱柱 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,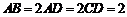 .
.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
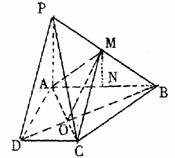 4、已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=
4、已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=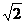 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
(Ⅰ)证明:平面PAD⊥PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分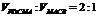
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD
是否平行面AMC.
赣马高级中学解答题专题训练17--------立体几何03
命题:樊继强 审核:刘卫兵 王怀学
2、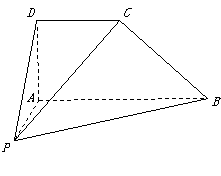 如图,在四棱锥P-ABCD中,CD//AB
, AD⊥AB , AD = DC = AB , BC⊥PC.
如图,在四棱锥P-ABCD中,CD//AB
, AD⊥AB , AD = DC = AB , BC⊥PC.
(1)求证:PA⊥BC ;(2)试在线段PB上找一点M,使CM // 平面PAD, 并说明理由.
1、如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=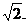
(1)求证:PA1⊥BC; (2)求证:PB1//平面AC1D;(3)求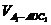
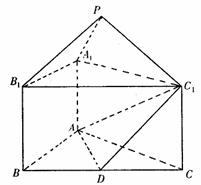
4. 如图为正方体ABCD-A1B1C1D1切去一个三棱锥B1-A1BC1后得到的几何体.(1) 画出该几何体的正视图;
(2) 若点O为底面ABCD的中心,求证:直线D1O∥平面A1BC1;
(3). 求证:平面A1BC1⊥平面BD1D.
赣马高级中学解答题专题训练16--------立体几何02
命题:樊继强 审核:刘卫兵 王怀学
3. 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,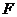 为
为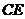 上的点,
上的点,
且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
2.
 一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点。
一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点。
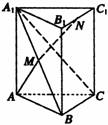 (Ⅰ)求证:MN//平面ACC1A1;
(Ⅰ)求证:MN//平面ACC1A1;
(Ⅱ)求证:MN⊥平面A1BC。
1、如图是某多面体的三视图,如果图中每个正方形的边长均为2
(1)请描述满足该三视图的一个几何的形状(或出画它的直观图);
(2)求你得到的几何体的体积;
(3)求你得到的几何体的表面积。
3.已知递增数列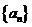 满足:
满足: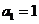 ,
,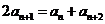
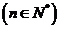 ,且
,且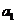 、
、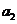 、
、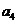 成等比数列。
成等比数列。
(I)求数列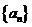 的通项公式
的通项公式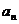 ;
;
(II)若数列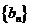 满足:
满足: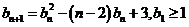 ,
, 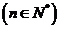 。
。
①用数学归纳法证明: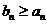 ;
;
②记 ,证明:
,证明: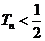 。
。
解:(I)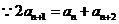 ,∴数列
,∴数列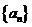 为等差数列,设公差为
为等差数列,设公差为
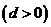 。
。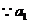 、
、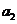 、
、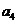 成等比数列,∴
成等比数列,∴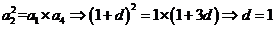
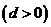
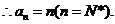
(II)①即证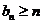
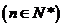 ,用数学归纳法证明如下:(1)当
,用数学归纳法证明如下:(1)当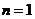 时,
时,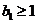 ,原不等式成立;
,原不等式成立;
(2)假设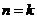 时原不等式成立,即
时原不等式成立,即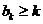
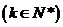 ,那么当
,那么当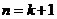 时,
时,
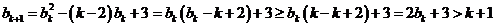
∴当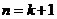 时原不等式也成立
时原不等式也成立
由(1)(2)可知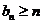
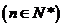 ②证明:由
②证明:由
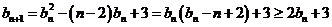 ,而
,而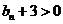 ,∴
,∴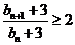 ∴
∴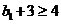 ,
,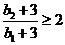 ,
, ,
,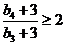 ,
, ,
,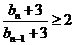 ∴
∴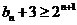
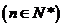 ,∴
,∴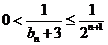 ∴
∴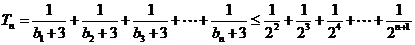 ∴
∴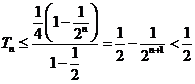 ∴
∴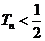
 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com