7．某网球中心欲建连成片的网球场数块，用128万元购买土地10000平方米，该中心每块球场的建设面积为1000平方米，球场的总建筑面积的每平方米的平均建设费用与球场数有关，当该中心建球场x块时，每平方米的平均建设费用(单位：元)可近似地用f(x)＝800(1+lnx)来刻画．为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，该网球中心应建几个球场?

6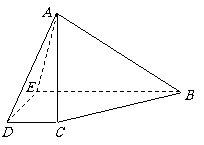．如图，在四棱锥A－BCDE中，底面BCDE是直角梯形，∠BED＝90°，BE∥CD，AB＝6，BC＝5，＝，侧面ABE^底面BCDE．且ÐBAE＝90°．

(1)求证：平面ADE^平面ABE；

(2)过点D作平面a∥平面ABC，分别与BE，AE

交于点F，G，求△DFG的面积．

5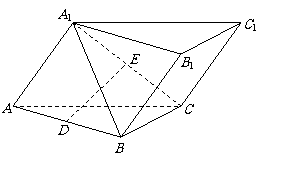．如图，在三棱柱ABC－A₁B₁C₁中，AB＝AC＝2AA₁，ÐBAA₁＝ÐCAA₁＝60°，D，E分别为AB，A₁C中点．

(1)求证：DE∥平面BB₁C₁C；

(2)求证：BB₁^平面A₁BC．

4．计算：2sin20°+cos10°+tan20°×sin10°．

3．已知函数f(x)＝sin⁴wx+cos⁴wx的相邻对称轴之间的距离为．(1)求正数w的值；(2)求函数g(x)＝2f(x)+sin²(x+)的最大值及取到最大值时x的值．

2．已知a＝(cosa，sina)，b＝(cosb，sinb)，c＝(1，7sina)，且0＜b＜a＜．

若a×b＝，a∥c．(1)求tanb的值；(2)求cos(2a－b)的值．

1．设锐角△ABC内角A，B，C的对边分别为a，b，c．已知边a＝2，△ABC的面积S＝(b²+c²－a²)．求：(1)内角A；(2)周长l的取值范围．

10．函数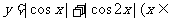R) 的最小值是　　　　　 ．

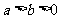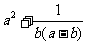*11．设 ，那么 　的最小值是　　　　　 ．

*12．已知等比数列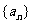的公比为q，前n项和S_n＞0(n＝1，2，

3，…)，则q的取值范围是 　．

*13．已知正四棱锥的高为4cm，一个侧面三角形的面积

是15cm²，则该四棱锥的体积是____cm³．

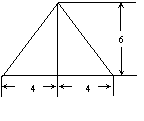
*14．已知一个正六棱锥的左视图如图所示(单位：cm)，

则此正六棱台的体积等于_______cm³．

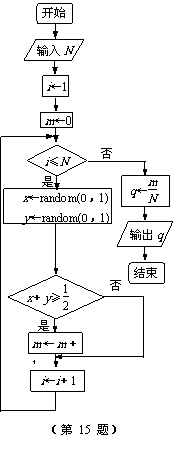
**15．下列程序框图(假设函数random(0，1)是产生随机数的函

数，它能随机产生区间(0，1)内的任何一个实数)．随着输入N

的不断增大，输出的值q会在某个常数p附近摆动并趋于稳定，则

常数p的值是　　 　　．

**16．设F₁、F₂为双曲线的左、右焦点，P为双曲线右支上任一点，若的最小值恰是实轴长的4倍，则该双曲线离心率的取值范围是　　　　 ．

**17．用一张正方形包装纸把一个棱长为1的正四面体礼品盒包住(按常规，包装纸可折叠，但不能剪开)，则包装纸的最小面积是__________．

**18．抛物线顶点为O，焦点为F，M是抛物线上的动点，则的最大值为　 　　　　．

9．在数列{a_n}中，a₁=2，a_n+1＝1－a_n(n∈N^*)，设S_n为数列{a_n}的前n项和，则S₂₀₀₇－2S₂₀₀₈+S₂₀₀₉=　 　　　　．

8．若直线l与圆C：x²+y²－4y+2＝0相切，且与两条坐标轴围成一个等腰直角三角形，则此三角形的面积为　　　　　 ．