
题目列表(包括答案和解析)
4、(1)证明: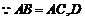 为
为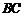 中点
中点 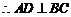 ,
,
又直三棱柱中: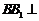 底面
底面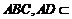 底面
底面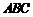 ,
,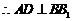 ,
,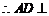 平面
平面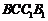 ,
,
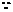
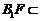 平面
平面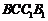
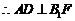 .在 矩形
.在 矩形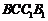 中:
中: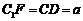 ,
,
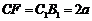
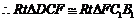 ,
,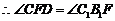
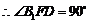 ,即
,即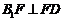 ,
, 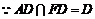 ,
,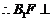 平面
平面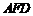 ;
;
(2)解: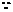
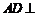 平面
平面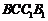
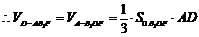
=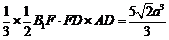 ;
;
(3)当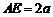 时,
时,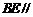 平面
平面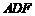 .
.
证明:连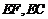 ,设
,设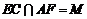 ,连
,连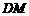 ,
,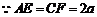
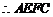 为矩形,
为矩形,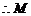 为
为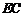 中点,
中点,
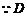 为
为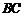 中点,
中点,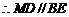 ,
,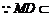 平面
平面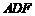 ,
,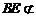 平面
平面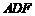
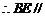 平面
平面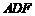 .
.
赣马高级中学解答题专题训练--------立体几何04
3、(Ⅰ)证明:因为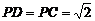 ,
,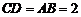 ,所以
,所以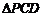 为等腰直角三角形,所以
为等腰直角三角形,所以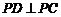 .因为
.因为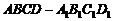 是一个长方体,所以
是一个长方体,所以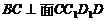 ,而
,而 ,所以
,所以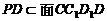 ,所以
,所以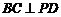 .
.
因为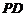 垂直于平面
垂直于平面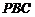 内的两条相交直线
内的两条相交直线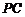 和
和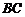 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得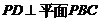 .
.
(Ⅱ)解:当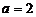 时,
时,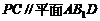 .当
.当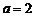 时,四边形
时,四边形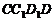 是一个正方形,所以
是一个正方形,所以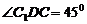 ,而
,而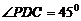 ,所以
,所以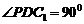 ,所以
,所以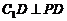 .
.
而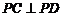 ,
,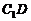 与
与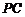 在同一个平面内,所以
在同一个平面内,所以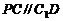 . 而
. 而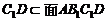 ,所以
,所以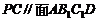 ,所以
,所以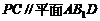 .
.
2、(1)证明:由直四棱柱,得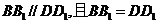 ,
,
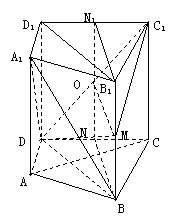 所以
所以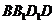 是平行四边形,所以
是平行四边形,所以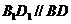 …………(3分)
…………(3分)
而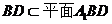 ,
,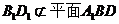 ,所以
,所以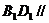 面
面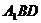 …(5分)
…(5分)
(2)证明:因为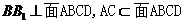 , 所以
, 所以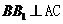 (7分)
(7分)
又因为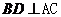 ,且
,且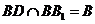 ,所以
,所以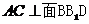 …(9分)
…(9分)
而 ,所以
,所以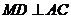 ……………(10分)
……………(10分)
(3)当点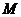 为棱
为棱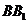 的中点时,平面
的中点时,平面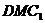
 平面
平面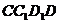 ,取DC的中点N,
,取DC的中点N,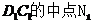 ,连结
,连结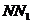 交
交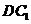 于
于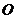 ,连结
,连结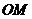 .
.
因为N是DC中点,BD=BC,所以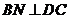 ;
;
又因为DC是面ABCD与面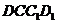 的交线,而面ABCD⊥面
的交线,而面ABCD⊥面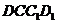 ,
,
所以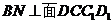 又可证得,
又可证得,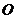 是
是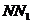 的中点,
的中点,
所以BM∥ON且BM=ON,即BMON是平行四边形,
所以BN∥OM,所以OM 平面
平面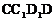 ,因为OM?面DMC1,所以平面
,因为OM?面DMC1,所以平面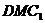
 平面
平面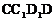
1、解:(Ⅰ) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,又∵DC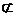 平面ABE,EB
平面ABE,EB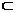 平面ABE,∴DC∥平面ABE……(4分)
平面ABE,∴DC∥平面ABE……(4分)
(Ⅱ)∵DC⊥平面ABC,∴DC⊥AF,又∵AF⊥BC,∴AF⊥平面BCDE……(8分)
(Ⅲ)由(2)知AF⊥平面BCDE,∴AF⊥EF,在三角形DEF中,由计算知DF⊥EF,
∴EF⊥平面AFD,又EF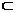 平面AFE,∴平面AFD⊥平面AFE.……(14分)
平面AFE,∴平面AFD⊥平面AFE.……(14分)
4、(I)证明:依题意知: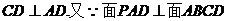
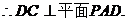
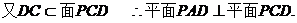
(II)由(I)知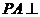 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD.
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则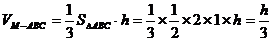
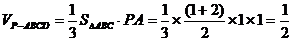
要使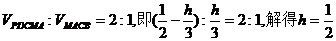
即M为PB的中点.
(Ⅲ)连接BD交AC于O,因为AB//CD,AB=2,CD=1,由相似三角形易得BO=2OD
∴O不是BD的中心
又∵M为PB的中点
∴在△PBD中,OM与PD不平行
∴OM所以直线与PD所在直线相交
又OM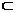 平面AMC
平面AMC
∴直线PD与平面AMC不平行.
赣马高级中学解答题专题训练--------立体几何03答案
3、证明:(Ⅰ)
直棱柱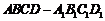 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,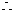 BB1⊥AC.
BB1⊥AC.
又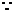 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,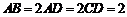 ,∴
,∴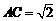 ,∠CAB=45°,∴
,∠CAB=45°,∴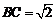 ,
,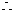 BC⊥AC.又
BC⊥AC.又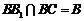 ,
,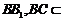 平面BB1C1C,
平面BB1C1C,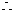 AC⊥平面BB1C1C.
AC⊥平面BB1C1C.
(Ⅱ)存在点P,P为A1B1的中点.证明:由P为A1B1的中点,有PB1‖AB,且PB1=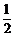 AB.
AB.
又∵DC‖AB,DC=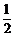 AB,
AB,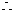 DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.分
又CB1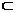 面ACB1,DP
面ACB1,DP 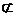 面ACB1,
面ACB1,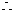 DP‖面ACB1.
DP‖面ACB1.
同理,DP‖面BCB1.
2、(1)连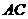 ,在四边形ABCD中,
,在四边形ABCD中,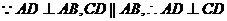 .
.
设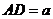 ,
,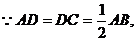
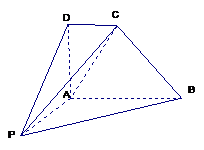
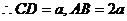 .
.
 在
在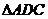 中,
中,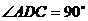 ,
,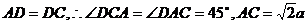
在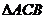 中,
中,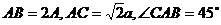
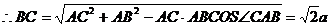 .
.
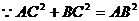 ,
,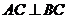 ………………………3分
………………………3分
又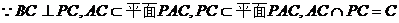 ,
,
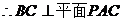
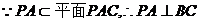 .
.
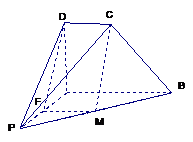 (2)当
(2)当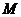 为
为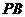 的中点时,
的中点时,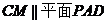 ,取
,取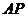 的中点
的中点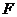 ,
,
连结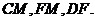 则
则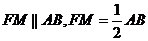 .
.
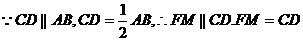
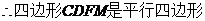 ,
,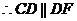
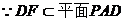 ,
,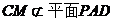 ,
,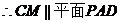 .
.
1、(1)证明:取B1C1的中点Q,连结A1Q,PQ,∴B1C1⊥A1Q,B1C1⊥PQ,∴B1C1⊥平面AP1Q,
∴B1C1⊥PA1,
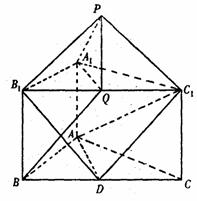 ∵BC∥B1C1,∴BC⊥PA1.
∵BC∥B1C1,∴BC⊥PA1.
(2)连结BQ,在△PB1C1中,PB1=PC1=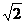 ,B1C1=2,Q为中点,
,B1C1=2,Q为中点,
∴PQ=1,∴BB1=PQ,∴BB1∥PQ,∴四边形BB1PQ为平行四边形,
∴PB1∥BQ.
∴BQ∥DC1,∴PB1∥DC1,又∵PB1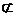 面AC1D,、
面AC1D,、
∴PB1∥平面AC1D.(3)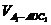 =
=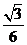
4、解:(1)该几何体的正视图为:
(2)将其补成正方体ABCD-A1B1C1D1,设B1D1和A1C1交于点O1,连接O1B,
依题意可知,D1O1∥OB,且D1O1=OB,即四边形D1OB O1为平行四边形,
则D1O∥O1B,因为BO1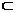 平面BA1C1,D1O
平面BA1C1,D1O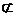 平面BA1C1,所以有直线D1O∥平面BA1C1;
平面BA1C1,所以有直线D1O∥平面BA1C1;
(3)在正方体ABCD-A1B1C1D1中,DD1⊥平面A1B1C1D1,
则DD1⊥A1C1 另一方面,B1D1⊥A1C1
 又∵DD1∩B1D1=
D1,∴A1C1⊥平面BD1D,
又∵DD1∩B1D1=
D1,∴A1C1⊥平面BD1D,
∵A1C1 平面A1BC1,则平面A1BC1⊥平面BD1D.
平面A1BC1,则平面A1BC1⊥平面BD1D.
赣马高级中学解答题专题训练--------立体几何02答案
3、(1)证明: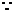
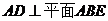 ,
,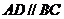 ∴
∴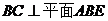 ,则
,则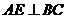 (2分)
(2分)
又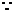
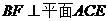 ,则
,则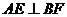 ∴
∴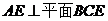 又
又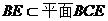 ∴
∴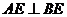
(2)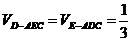 ×
×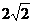 ×
×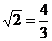
(3)在三角形ABE中过M点作MG∥AE交BE于G点,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,则由比例关系易得CN=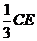
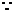 MG∥AE MG
MG∥AE MG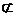 平面ADE, AE
平面ADE, AE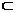 平面ADE,
平面ADE, MG∥平面ADE同理,
GN∥平面ADE
MG∥平面ADE同理,
GN∥平面ADE
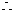 平面MGN∥平面ADE 又MN
平面MGN∥平面ADE 又MN 平面MGN
平面MGN  MN∥平面ADE
MN∥平面ADE
 N点为线段CE上靠近C点的一个三等分点
N点为线段CE上靠近C点的一个三等分点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com