
题目列表(包括答案和解析)
9.(理)已知有相同两焦点F1、F2的椭圆 + y2=1(m>1)和双曲线 - y2=1(n>0),P是它们
的一个交点,则ΔF1PF2的形状是 ( )
A.锐角三角形 B.直角三角形 C.钝有三角形 D.随m、n变化而变化
(文)已知有相同两焦点F1、F2的椭圆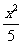 + y2=1和双曲线
+ y2=1和双曲线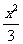 - y2=1,P是它们的一个交点,
- y2=1,P是它们的一个交点,
则ΔF1PF2的形状是 ( )
A.锐角三角形 B.直角三角形 C.钝有三角形 D.等腰三角形
8.函数y=x3-2ax+a在(0,1)内有极小值,则实数a的取值范围是 ( )
A.(0,3) B.(-∞,3) C.(0,+∞) D.(0,)
7.在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其它10个小长方形面积和的,且样本容量为160,则中间一组的频数为 ( )
A.32 B.0.2 C.40 D.0.25
6.已知球的表面积为20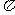 ,球面上有A、B、C三点,如果AB=AC=2,BC=2
,球面上有A、B、C三点,如果AB=AC=2,BC=2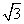 ,则球心
,则球心
到平面ABC的距离为 ( )
A.1 B.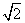 C.
C.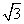 D.2
D.2
5.设四面体的四个面的面积分别为S1,S2,S3,S4,它们的最大值为S,记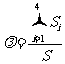 ,
,
则有 ( )
A.2<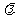 ≤4 B.3<
≤4 B.3<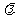 ≤4 C.2.5<
≤4 C.2.5<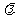 ≤4.5 D.3.5<
≤4.5 D.3.5<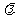 ≤5.5
≤5.5
4.已知当x∈R时,函数y=f(x)满足f(2.1+x)=f(1.1+x) + ,且f(1)=1,则f(100)
的值为 ( )
A. B. C.34 D.
3.已知f(x)=sin(x+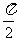 ),g(x)=cos(x-
),g(x)=cos(x-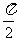 ),则下列结论中正确的是 ( )
),则下列结论中正确的是 ( )
A.函数y=f(x)·g(x)的最大值为1
B.函数y=f(x)·g(x)的对称中心是(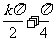 ,0),
,0),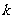 ∈Z
∈Z
C.当x∈[-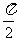 ,
,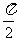 ]时,函数y=f(x)·g(x)单调递增
]时,函数y=f(x)·g(x)单调递增
D.将f(x)的图象向右平移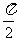 单位后得g(x)的图象
单位后得g(x)的图象
2.(理)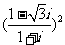 等于
( )
等于
( )
A.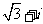 B.
B.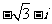 C.
C.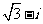 D.
D.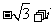
(文)函数y=(x+1)2(x-1)在x=1处的导数等于 ( )
A.1 B.2 C.3 D.4
1.已知M={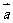 |
|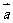 =(1,2)+
=(1,2)+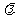 (3,4),
(3,4),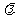 ∈R},N={
∈R},N={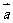 |
|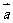 =(-2,-2)+μ(4,5),μ∈R},则
=(-2,-2)+μ(4,5),μ∈R},则
M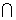 N=
( )
N=
( )
A.{(1,1)} B.{(1,1),(-2,-2)} C.{(-2,-2)} D.φ
19、(本小题满分12分)
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示。
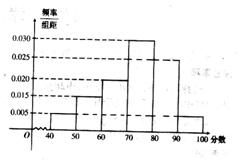 (1)估计这次测试数学成绩的平均分;
(1)估计这次测试数学成绩的平均分;
(2)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率
(20)(本小题满分12分)
已知等差数列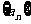 的前
的前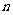 项和为
项和为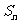 ,公差
,公差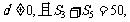
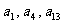 成等比数列.
成等比数列.
(Ⅰ)求数列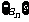 的通项公式;
的通项公式;
(Ⅱ)若从数列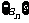 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……,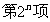 ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列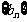 ,记该数列的前
,记该数列的前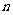 项和为
项和为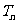 ,求
,求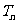 的表达式.
的表达式.
(21)(本小题满分12分)
已知定义在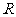 上的函数
上的函数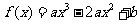
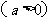 在区间
在区间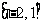 上的最大值是5,最小值是-11.
上的最大值是5,最小值是-11.
(Ⅰ)求函数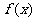 的解析式;
的解析式;
(Ⅱ)若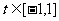 时,
时,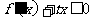 恒成立,求实数
恒成立,求实数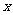 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知直线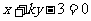 所经过的定点
所经过的定点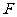 恰好是椭圆
恰好是椭圆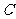 的一个焦点,且椭圆
的一个焦点,且椭圆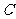 上的点到点
上的点到点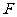 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆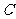 的标准方程;
的标准方程;
(Ⅱ)已知圆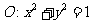 ,直线
,直线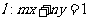 .试证明:当点
.试证明:当点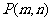 在椭圆
在椭圆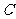 上运动时,直线
上运动时,直线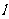 与圆
与圆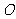 恒相交,并求直线
恒相交,并求直线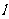 被圆
被圆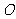 所截得弦长
所截得弦长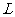 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com