17．已知数列{a_n}、{b_n}满足a₁=2 ，b₁=1，且(n≥2)，l+m＝1．

(1)令c_n= a_n+b_n，求数列{c_n}的通项公式；

(2)当l－m＝时，求数列{a_n}的通项公式．

16．已知函数f(x)＝+．

(1)求函数f(x)的值域；

(2)设F(x)＝m+f(x)，记F(x)的最大值为g(m)，求g(m)的表达式．

15．函数y＝f(x)在区间(0，+∞)内的导函数f ¢(x)是减函数，且f ¢(x)＞0 ．

设x₀∈(0，+∞)，y＝kx+m是曲线y＝f(x)在点(x₀，f(x₀))处的切线方程，并设函数g(x)＝kx+m．

(1)用x₀、f(x₀)、f ¢(x₀)表示m；

(2)证明：当x₀∈(0，+∞)时，g(x)≥f(x)．

14．已知函数f(x)＝x⁴+ax³+2x²+b(x∈R)，其中a，b∈R．

(1)当a＝－时，讨论函数f(x)的单调性；

(2)若函数f(x)仅在x＝0处有极值，求a的取值范围；

(3)若对于任意的a∈[－2，2]，不等式f(x)≤1在[－1，1]上恒成立，求b的取值范围．

13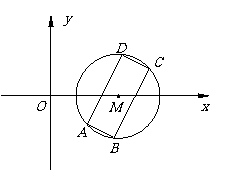．如图，已知矩形ABCD的四个顶点在圆M：(x－4)²+y²＝r²(r＞0)上，且直线AD的斜率为2，AD＝3AB．

(1)求矩形对角线AC，BD所在直线的方程；

(2)若以原点O为顶点，焦点在x轴上的抛物

线过点A，B，求此抛物线的方程．

12．如图，已知椭圆+＝1(a＞0)上两点A(x₁，y₁)，B (x₂，y₂)，x轴上两点M(1，0)，N(－1，0)．

(1)若tan∠ANM＝－2，tan∠AMN＝，求该椭圆的方程；

(2)若→＝－2→，且0＜x₁＜x₂，

求椭圆的离心率e的取值范围．

11．已知椭圆C：+＝1(a＞b＞0)，直线l为圆O：x²+y²＝b²的一条切线，且经过椭圆的右焦点，记椭圆离心率为e．

(1)若直线l的倾斜角为，求e的值；

(2)是否存在这样的e，使得原点O关于直线l的对称点恰好在椭圆C上？若存在，请求出e的值；若不存在，请说明理由．

10．一个截面为抛物线形的旧河道，河口宽AB＝4米，河深2米，现要将其截面改造为等腰梯形，要求河道深度不变，而且施工时只能挖土，不准向河道填土，

试求当截面梯形的下底长为多少米时，才能使挖出的土最少？

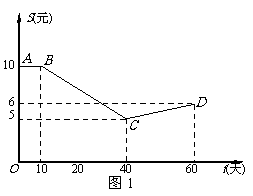
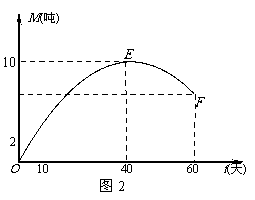
9．时值5月，荔枝上市．某市水果市场由历年的市场行情得知，从5月10日起的60天内，荔枝的售价S(t)(单位：元／kg)与上市时间t(单位：天)的关系大致可用如图1所示的折线ABCD表示，每天的销售量M(t)(单位：吨)与上市时间t(单位：天)的关系大致可用如图2所示的抛物线段OEF表示，其中O为坐标原点，E是抛物线的顶点．

(1)请分别写出S(t)，M(t)关于t的函数关系式；

(2)在这60天内，该水果市场哪天的销售额最大？

8．某观测站C在A城的南偏西20^o的方向，由A城出发有一条公路，公路的走向是南偏东40^o，在C处测得距离为31km的公路上B处，有一人正沿着公路向A城走来，他走了20km后到达D处，此时C，D之间相距21km，问此人还要走多少路才能到达A城？