
题目列表(包括答案和解析)
20.解:(Ⅰ)因为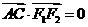 ,所以有
,所以有
所以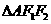 为直角三角形;
为直角三角形;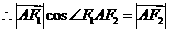 …………………………2分
…………………………2分
则有
所以,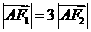 …………………………3分
…………………………3分
又 ,
,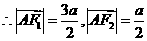 ………………………4分
………………………4分
在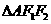 中有
中有
即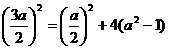 ,解得
,解得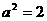
所求椭圆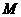 方程为
方程为 …………………………6分
…………………………6分
(Ⅱ)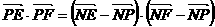
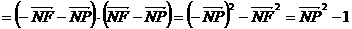
从而将求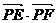 的最大值转化为求
的最大值转化为求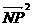 的最大值
…………………8分
的最大值
…………………8分
是椭圆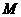 上的任一点,设
上的任一点,设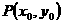 ,则有
,则有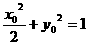 即
即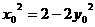
又 ,所以
,所以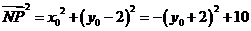 ………………10分
………………10分
而 ,所以当
,所以当 时,
时,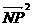 取最大值
取最大值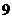
故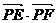 的最大值为
的最大值为 ……………………12分
……………………12分
20.(本小题满分12分)已知 均在椭圆
均在椭圆 上,直线
上,直线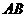 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点 、
、 ,当
,当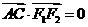 时,有
时,有 .
.
(Ⅰ)求椭圆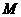 的方程;
的方程;
(Ⅱ)设是椭圆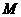 上的任一点,
上的任一点,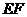 为圆
为圆 的任一条直径,求
的任一条直径,求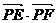 的最大值.
的最大值.
19.解:(Ⅰ)已知函数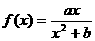 ,
,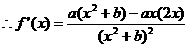 …………1分
…………1分
又函数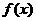 在
在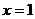 处取得极值2,
处取得极值2,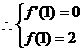 …………2分
…………2分
即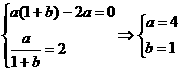
 …………………4分
…………………4分
(Ⅱ)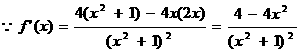 由
由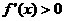 ,得
,得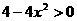 ,即
,即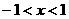
所以 的单调增区间为(-1,1) ………………… 6分
的单调增区间为(-1,1) ………………… 6分
因函数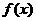 在(m,2m+1)上单调递增,
在(m,2m+1)上单调递增,
则有 , …………7分
, …………7分
解得 即
即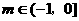 时,函数
时,函数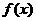 在(m,2m+1)上为增函数 ………8分
在(m,2m+1)上为增函数 ………8分
(Ⅲ)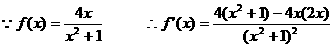
直线l的斜率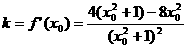 …………9分
…………9分
即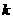
 令
令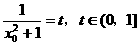 , …………10分
, …………10分
则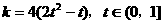
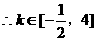 即直线l的斜率k的取值范围是
即直线l的斜率k的取值范围是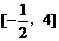 ……………12分
……………12分
19.(本小题满分12分)已知函数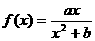 ,在
,在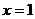 处取得极值为.
处取得极值为.
(Ⅰ)求函数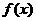 的解析式;
的解析式;
(Ⅱ)若函数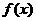 在区间
在区间 上为增函数,求实数的取值范围;
上为增函数,求实数的取值范围;
(Ⅲ)若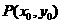 为
为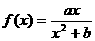 图象上的任意一点,直线
图象上的任意一点,直线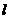 与
与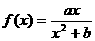 的图象相切于点,求直线
的图象相切于点,求直线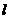 的斜率的取值范围.
的斜率的取值范围.
22.(本小题满分12分)
64个正数排成8行8列的方阵,其中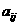 (1≤i≤8,1≤j≤8,i,j∈N﹡)表示位于第i行第j列的正数:
(1≤i≤8,1≤j≤8,i,j∈N﹡)表示位于第i行第j列的正数:
a11 a12 a13 … a18
a21 a22 a23 … a28
……………………………………
a81 a82 a83 … a88
已知每一行的数成等差数列,每一列的数成等比数列,且各列的公比都等于q.若a11=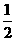 ,a24=1,a32=
,a24=1,a32= ,
,
(1)求{ 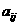 }的通项公式;
}的通项公式;
(2)记第k行各项的和为Ak ,求A1的值及数列{Ak}的通项公式;
(3)若Ak<1,求k的值.



21.(本小题满分12分)
已知函数f(x)=lnx,g(x)=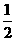 ax2+bx(a≠0)
ax2+bx(a≠0)
(1)若a=-2时,函数h(x)=f(x)-g(x),在其定义域上是增函数,求b的取值范围;
(2)在(1)的结论下,设函数 (x)=
(x)=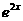 +b
+b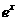 ,x∈[0,ln2],求函数
,x∈[0,ln2],求函数 (x)的最
(x)的最
小值;
(3)设函数f(x)的图象C1与函数g(x)的图象C2交于P、Q,过线段PQ的中点R
作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与
C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。
20.(本小题满分12分)
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线x-y+2 =0
=0
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线y=kx+m(k≠0)相交于不同的两点M、N.当|AM |=|AN|时,求m的取值范围.
2. 濮阳市二模
21.解:(1)设椭圆方程为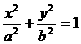 (a>b>0),
(a>b>0),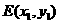
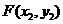
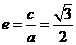 令
令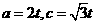 则
则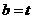
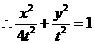 …………2分
…………2分
由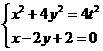 得:
得: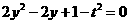 ………………………………
4分
………………………………
4分
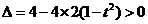
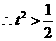
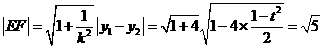
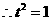
椭圆C的方程是: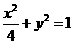 …………………………………… 7分
…………………………………… 7分
(2) 当直线AB不垂直于x轴时,设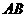 :
: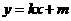
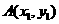
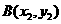
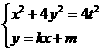 得
得
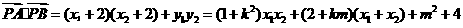
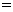
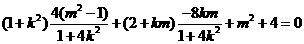 …………………… 10分
…………………… 10分


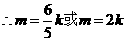
当 时,
时,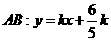 恒过定点
恒过定点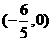
当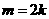 时,
时,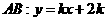 恒过定点
恒过定点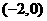 ,不符合题意舍去 … 12分
,不符合题意舍去 … 12分
当直线AB垂直于x轴时,若直线AB: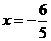 则AB与椭圆C相交于
则AB与椭圆C相交于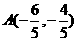 ,
,
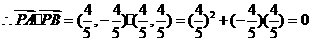
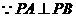 ,满足题意
,满足题意
综上可知,直线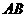 恒过定点,且定点坐标为
恒过定点,且定点坐标为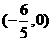 ……………… 14分
……………… 14分
21.(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率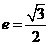 .直线
.直线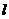 :
: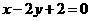 与椭圆C相交于
与椭圆C相交于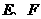 两点, 且
两点, 且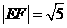 .(1)求椭圆C的方程;(2)点P(
.(1)求椭圆C的方程;(2)点P(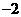 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当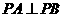 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com