
题目列表(包括答案和解析)
21.(本小题满分12分)
已知函数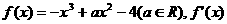 是
是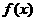 的导函数。
的导函数。
(1)当a=2时,对于任意的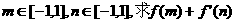 的最小值;
的最小值;
(2)若存在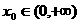 ,使
,使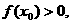 求a的取值范围。
求a的取值范围。
20.解:(1)由已知得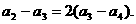
从而得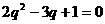
解得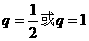 (舍去) …………4分
(舍去) …………4分
所以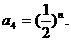 …………6分
…………6分
(2)由于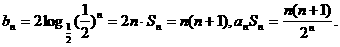
因此所证不等式等价于: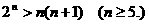
①当n=5时,因为左边=32,右边=30,所以不等式成立;
②假设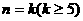 时不等式成立,即
时不等式成立,即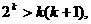
两边同乘以2得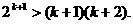
这说明当n=k+1时也不等式成立。
由①②知,当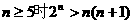 成立。
成立。
因此,当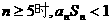 成立。 …………12分
成立。 …………12分
20.(本小题满分12分)
已知等比数列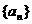 中,
中,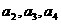 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且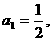 公比
公比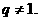
(1)求数列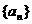 的通项公式;
的通项公式;
(2)已知数列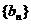 满足
满足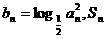 是数列
是数列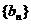 的前n项和,
的前n项和,
求证:当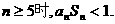
1. 聊城一模
20.(本小题满分16分)
设函数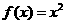 ,
,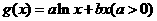 .
.
(Ⅰ)若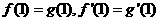 ,求
,求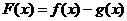 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数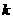 和
和 ,使得
,使得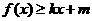 和
和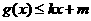 ?若存在,求出
?若存在,求出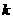 和
和 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设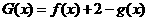 有两个零点
有两个零点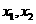 ,且
,且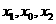 成等差数列,试探究
成等差数列,试探究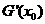 值的符号.
值的符号.

图表 2高 考 资 源 网



19.(本小题满分16分)
设等比数列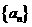 的首项为
的首项为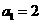 ,公比为
,公比为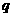 (
(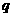 为正整数),且满足
为正整数),且满足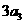 是
是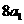 与
与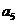 的等差中项;数列
的等差中项;数列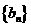 满足
满足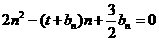 (
(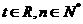 ).
).
(Ⅰ)求数列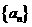 的通项公式;
的通项公式;
(Ⅱ)试确定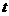 的值,使得数列
的值,使得数列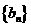 为等差数列;
为等差数列;
(Ⅲ)当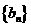 为等差数列时,对每个正整数
为等差数列时,对每个正整数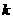 ,在
,在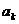 与
与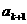 之间插入
之间插入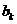 个2,得到一个新数列
个2,得到一个新数列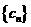 . 设
. 设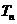 是数列
是数列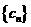 的前
的前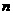 项和,试求满足
项和,试求满足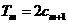 的所有正整数
的所有正整数 .
.
18.(本小题满分16分)
已知在△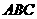 中,点
中,点 、
、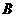 的坐标分别为
的坐标分别为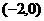 和
和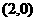 ,点
,点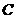 在
在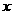 轴上方.
轴上方.
(Ⅰ)若点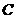 的坐标为
的坐标为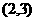 ,求以
,求以 、
、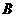 为焦点且经过点
为焦点且经过点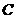 的椭圆的方程;
的椭圆的方程;
(Ⅱ)若∠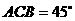 ,求△
,求△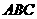 的外接圆的方程;
的外接圆的方程;
(Ⅲ)若在给定直线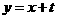 上任取一点
上任取一点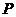 ,从点
,从点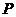 向(Ⅱ)中圆引一条切线,切点为
向(Ⅱ)中圆引一条切线,切点为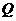 . 问是否存在一个定点
. 问是否存在一个定点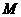 ,恒有
,恒有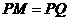 ?请说明理由.
?请说明理由.
3. 盐城一模
21. [解析](1)令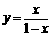 ,解得
,解得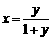 ,由
,由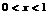 ,解得
,解得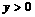 ,
,
∴函数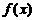 的反函数
的反函数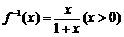 ,则
,则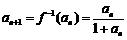 ,得
,得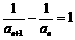 .
.
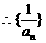 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故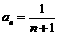 .
……3分
.
……3分
(2)∵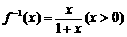 ,∴
,∴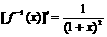 ,
,
∴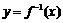 在点
在点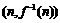 处的切线方程为
处的切线方程为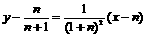 ,
,
令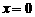 , 得
, 得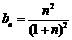 ,∴
,∴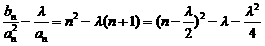 ,
,
∵仅当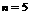 时取得最小值,∴
时取得最小值,∴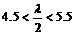 ,解之
,解之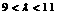 ,
,
∴的取值范围为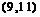 .
……7分
.
……7分
(3)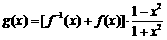
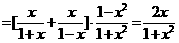 ,
,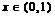 .
.
则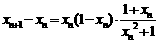 ,
,
因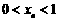 ,则
,则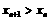 ,显然
,显然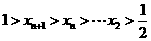 .
.
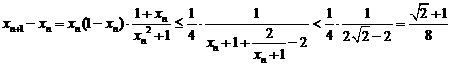
∴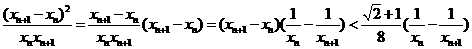
∴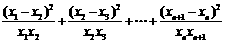
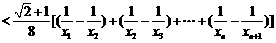
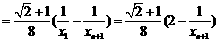
∵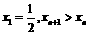 ,∴
,∴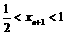 ,
,
∴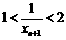 ,∴
,∴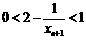
∴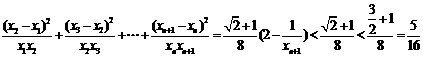 . ……12分
. ……12分
21.(本小题满分12分)已知函数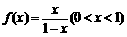 的反函数为
的反函数为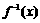 ,数列
,数列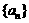 和
和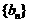 满足:
满足: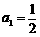 ,
,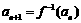 ,函数
,函数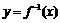 的图象在点
的图象在点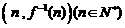 处的切线在轴上的截距为
处的切线在轴上的截距为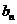 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若数列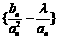 的项仅
的项仅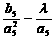 最小,求的取值范围;
最小,求的取值范围;
(3)令函数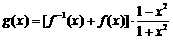 ,
,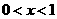 ,数列
,数列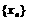 满足:
满足: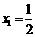 ,
,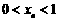 ,且
,且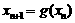 ,其中
,其中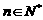 .证明:
.证明: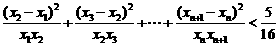 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com