4．已知定义在R上的函数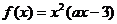，其中a为常数.(1)若x=1是函数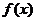的一个极值点，求a的值；(2)若函数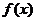在区间(－1，0)上是增函数，求a的取值范围；(3)若函数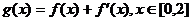，在x=0处取得最大值，求正数a的取值范围.

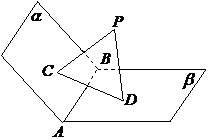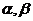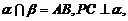
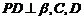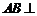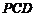3. 如图已知平面，且是垂足．(Ⅰ)求证：平面；(Ⅱ)若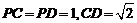，试判断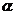平面与平面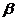的位置关系，并证明你的结论．

1．设向量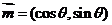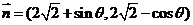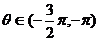，，，若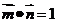，求：(1)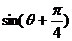的值；　　　 (2)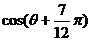的值．

2某公司欲建连成片的网球场数座，用128万元购买土地10000平方米，该球场每座的建筑面积为1000平方米，球场的总建筑面积的每平方米的平均建筑费用与球场数有关，当该球场建n个时，每平方米的平均建筑费用用f(n)表示，且f(n)=f(m )(1+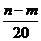)(其中n＞m,n∈N)，又知建五座球场时，每平方米的平均建筑费用为400元，为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和)，公司应建几个球场?

16、过点P(－3，0)且倾斜角为30°的直线和曲线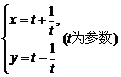相交于A、B两点．求线段AB的长．

15．已知椭圆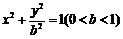的左焦点为F，左、右顶点分别为A、C，上顶点为B．过F、B、C作⊙P，其中圆心P的坐标为(m，n)．(Ⅰ)当m+n>0时，求椭圆离心率的范围；

(Ⅱ)直线AB与⊙P能否相切？证明你的结论．

14．已知△ABC三边a，b，c的长都是整数，且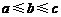，如果b＝m(mN*)，则这样的三角形共有　　　　 个(用m表示)．

13．若不等式组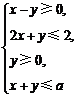 表示的平面区域是一个三角形及其内部，则a的取值范围是　 　　　　．

12．有一根长为6cm，底面半径为0.5cm的圆柱型铁管，用一段铁丝在铁管上缠绕4圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则铁丝的长度最少为　　　　 cm．

11．过抛物线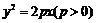的焦点F的直线l交抛物线于A、B两点，交准线于点C．若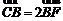，则直线AB的斜率为　 　　　．

10．已知函数f(x)＝log_a| x |在(0，+∞)上单调递增，则f(－2) 　　　f(a+1)．(填写“<”，“＝”，“>”之一)